题目内容
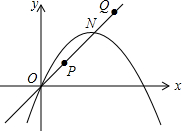 已知抛物线y=-
已知抛物线y=-| 1 |
| 2 |
| 2 |
考点:二次函数综合题
专题:
分析:由抛物线解析式可求出直线ON的解析式,由直线ON上有两个动点P和Q,且满足PQ=2
,在直线ON下方的抛物线上存在点M,使△PQM为等腰直角三角形,分两种情况①以PQ为斜边时②以PQ为直角边时,分别求解即可.
| 2 |
解答:解:∵抛物线y=-
x2+2x,点N为抛物线的顶点,
∴N(2,2)
∴直线ON的解析式为,y=x,
∵直线ON上有两个动点P和Q,且满足PQ=2
,在直线ON下方的抛物线上存在点M,使△PQM为等腰直角三角形,
①以PQ为斜边时:如图1,
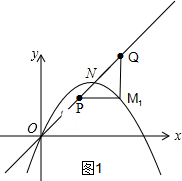
设M1(a1,b1)
∵PQ=2
,PM1=QM1,∠QM1P=90°,
∴a1-2=b1,
把M1(a1,a1-2)代入y=-
x2+2x,解得a1=1+
,a2=1-
,
∴M1(1+
,-1+
),M2(1-
,-1-
).
②以PQ为直角边时,如图2,
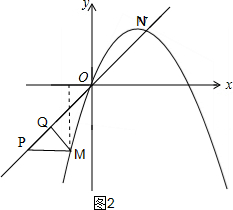
设M(a,b),
∵PQ=2
,
∴PM=4,PQ=QM4,∠PQM=90°,
∴a-4=b,
把M(a,a-4)代入y=-
x2+2x,解得a=4或-2,
∴M(-2,-6),或(4,0).
综上所述:点M的坐标为:(1+
,-1+
),(1-
,-1-
),(-2,-6),或(1-
,-1-
).
.故答案为:(1+
,-1+
),(1-
,-1-
),(-2,-6)或(4,0).
| 1 |
| 2 |
∴N(2,2)
∴直线ON的解析式为,y=x,
∵直线ON上有两个动点P和Q,且满足PQ=2
| 2 |
①以PQ为斜边时:如图1,

设M1(a1,b1)
∵PQ=2
| 2 |
∴a1-2=b1,
把M1(a1,a1-2)代入y=-
| 1 |
| 2 |
| 5 |
| 5 |
∴M1(1+
| 5 |
| 5 |
| 5 |
| 5 |
②以PQ为直角边时,如图2,

设M(a,b),
∵PQ=2
| 2 |
∴PM=4,PQ=QM4,∠PQM=90°,
∴a-4=b,
把M(a,a-4)代入y=-
| 1 |
| 2 |
∴M(-2,-6),或(4,0).
综上所述:点M的坐标为:(1+
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
.故答案为:(1+
| 5 |
| 5 |
| 5 |
| 5 |
点评:本题主要考查了二次函数与方程、几何知识的综合应用,解题的关键是将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识求解.

练习册系列答案
相关题目
如果分式方程
-
=1有增根,那么增根可能是( )
| 2x |
| x+3 |
| k |
| x2-9 |
| A、-3 | B、3 | C、3或-3 | D、0 |
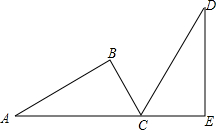 如图,在△ABC中,∠ACB=90°,∠A=30°,把△ABC绕点C旋转一定角度后得到△DEC,点A、C、E在同一直线上,则这个旋转角度为( )
如图,在△ABC中,∠ACB=90°,∠A=30°,把△ABC绕点C旋转一定角度后得到△DEC,点A、C、E在同一直线上,则这个旋转角度为( )| A、60° | B、90° |
| C、120° | D、150° |
 如图,△ABD为等边三角形,∠BCA=60°.求证:AC=BC+CD.
如图,△ABD为等边三角形,∠BCA=60°.求证:AC=BC+CD.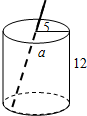 如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管长20,求吸管在罐外部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是
如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管长20,求吸管在罐外部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是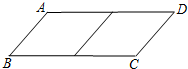 邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又剩下一个四边形,称为第二次操作;…依此类推,若第n次操作后,余下的四边形是菱形,则称原平行四边形为n阶准菱形.例如:如图,?ABCD中,若AB=1,BC=2,则?ABCD为1阶准菱形.
邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又剩下一个四边形,称为第二次操作;…依此类推,若第n次操作后,余下的四边形是菱形,则称原平行四边形为n阶准菱形.例如:如图,?ABCD中,若AB=1,BC=2,则?ABCD为1阶准菱形.
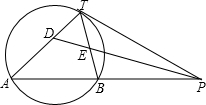 如图,PT是⊙O的切线,切点为T,直线PA与⊙O交于A、B两点,∠TPA的平分线分别交直线TA、TB于D、E两点.已知PT=2,PB=
如图,PT是⊙O的切线,切点为T,直线PA与⊙O交于A、B两点,∠TPA的平分线分别交直线TA、TB于D、E两点.已知PT=2,PB=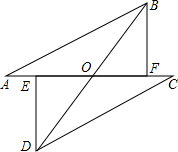 已知如图,线段AC,BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于点F,DE⊥AC于点E,AE=CF,求证:BD与EF互相平分.
已知如图,线段AC,BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于点F,DE⊥AC于点E,AE=CF,求证:BD与EF互相平分.