题目内容
 如图,正方形ABCD中,连接BD.点E在边BC上,且CE=2BE.连接AE交BD于F;连接DE,取BD的中点O;取DE的中点G,连接OG.下列结论:
如图,正方形ABCD中,连接BD.点E在边BC上,且CE=2BE.连接AE交BD于F;连接DE,取BD的中点O;取DE的中点G,连接OG.下列结论:①BF=OF;②OG⊥CD;③AB=5OG;④sin∠AFD=
2
| ||
| 5 |
其中正确结论的是
考点:四边形综合题
专题:
分析:由条件四边形ABCD是正方形可以得出AB=BC=CD=DA,AD∥BC,通过作辅助线制造直角三角形可以求出正弦值,利用三角形相似可以求出线段之间的关系,平行线的性质就可以求出相应的结论.
解答:解:∵CE=2BE,
∴
=
,
∴
=
.
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,
∴
=
,
∵AD∥BC,
∴△BFE∽△DFA,
∴
=
=
,
∵O是BD的中点,G是DE的中点,
∴OB=OD,OG=
BE,OG∥BC,
∴BF=OF,①正确,
OG⊥CD,②正确
OG=
BE=
×
BC=
BC=
AB,即AB=6OG,③错误,
连接OA,

∴OA=OB=2OF,OA⊥BD,
∴由勾股定理得;AF=
OF,
∴sin∠AFD=
=
=
,④正确,
故答案为①②④.
∴
| BE |
| CE |
| 1 |
| 2 |
∴
| BE |
| BC |
| 1 |
| 3 |
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,
∴
| BE |
| AD |
| 1 |
| 3 |
∵AD∥BC,
∴△BFE∽△DFA,
∴
| BF |
| DF |
| BE |
| AD |
| 1 |
| 3 |
∵O是BD的中点,G是DE的中点,
∴OB=OD,OG=
| 1 |
| 2 |
∴BF=OF,①正确,
OG⊥CD,②正确
OG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 6 |
连接OA,

∴OA=OB=2OF,OA⊥BD,
∴由勾股定理得;AF=
| 5 |
∴sin∠AFD=
| OA |
| AF |
| 2OF | ||
|
2
| ||
| 5 |
故答案为①②④.
点评:此题考查了相似三角形的判定与性质以及正方形的性质,三角形中位线的性质以及平行线的性质等知识.此题综合性很强,图形比较复杂,解题的关键是注意数形结合思想的应用与辅助线的准确选择.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
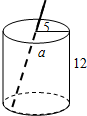 如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管长20,求吸管在罐外部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是
如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管长20,求吸管在罐外部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是
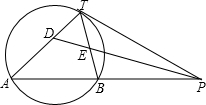 如图,PT是⊙O的切线,切点为T,直线PA与⊙O交于A、B两点,∠TPA的平分线分别交直线TA、TB于D、E两点.已知PT=2,PB=
如图,PT是⊙O的切线,切点为T,直线PA与⊙O交于A、B两点,∠TPA的平分线分别交直线TA、TB于D、E两点.已知PT=2,PB=
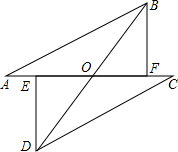 已知如图,线段AC,BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于点F,DE⊥AC于点E,AE=CF,求证:BD与EF互相平分.
已知如图,线段AC,BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于点F,DE⊥AC于点E,AE=CF,求证:BD与EF互相平分.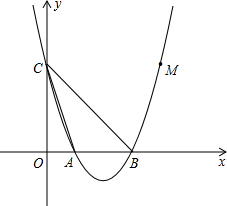 如图,已知抛物线y=a(x-1)(x-3)与x轴从左至右分别交于A、B两点,与y轴交于点C,且抛物线过点M(4,3),连接AC、BC.
如图,已知抛物线y=a(x-1)(x-3)与x轴从左至右分别交于A、B两点,与y轴交于点C,且抛物线过点M(4,3),连接AC、BC.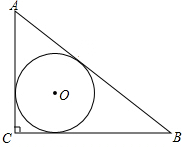 如图,Rt△ABC中,∠C=90°,AB,BC,CA的长分别为5,4,3,求△ABC的内切圆的半径r.
如图,Rt△ABC中,∠C=90°,AB,BC,CA的长分别为5,4,3,求△ABC的内切圆的半径r.