��Ŀ����
��ͼ�٣���֪���κ���y=a��x2-6x+8����a��0����ͼ����x��ֱ��ڵ�A��B����y�ύ�ڵ�C����D�������ߵĶ��㣮
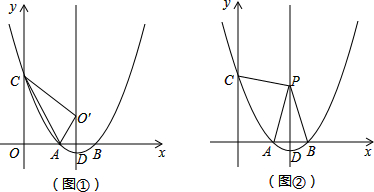
��1���������ߵĶԳ���Ϊ �� A������� ��B������� ��
��2������AC������OAC��ֱ��AC���ۣ�����O�Ķ�Ӧ��O��ǡ�����ڸ������ߵĶԳ����ϣ���ʵ��a��ֵ��
��3����ͼ�ڣ����P��m��n����n��0���Ǹ������߶Գ����ϵ�����һ�㣬����PA��PB��PC�����ʣ��Ƿ���ڵ�P��ʹ���߶�PA��PB��PC��PD�ij�����һ��ƽ���ı��ε������߳���Ӧ��ȣ������ڣ���д��һ������Ҫ��ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
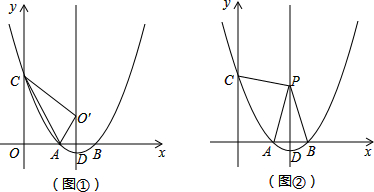
��1���������ߵĶԳ���Ϊ
��2������AC������OAC��ֱ��AC���ۣ�����O�Ķ�Ӧ��O��ǡ�����ڸ������ߵĶԳ����ϣ���ʵ��a��ֵ��
��3����ͼ�ڣ����P��m��n����n��0���Ǹ������߶Գ����ϵ�����һ�㣬����PA��PB��PC�����ʣ��Ƿ���ڵ�P��ʹ���߶�PA��PB��PC��PD�ij�����һ��ƽ���ı��ε������߳���Ӧ��ȣ������ڣ���д��һ������Ҫ��ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
���㣺���κ����ۺ���
ר�⣺
��������1�����������ߵĶԳ��ṫʽ���ɵ������ߵĶԳ��ᣬ���ݺ���ֵΪ��ʱ���ɵ�A��B������ꣻ
��2������ֱ�������ε����ʣ��ɵá�O��AM=60�㣬���ݷ��۵����ʣ��ɵá�OAC=��O��AC=60�㣬�ٸ���ֱ�������ε����ʣ��ɵô𰸣�
��3������ƽ���ı��ε��ж����ɵ�PC��PD�Ĺ�ϵ������PC=PD���ɵ÷��̣����ݽⷽ�̣��ɵô𰸣�
��2������ֱ�������ε����ʣ��ɵá�O��AM=60�㣬���ݷ��۵����ʣ��ɵá�OAC=��O��AC=60�㣬�ٸ���ֱ�������ε����ʣ��ɵô𰸣�
��3������ƽ���ı��ε��ж����ɵ�PC��PD�Ĺ�ϵ������PC=PD���ɵ÷��̣����ݽⷽ�̣��ɵô𰸣�
��� �⣺��1�����κ���y=a��x2-6x+8���ĶԳ�����x=-
�⣺��1�����κ���y=a��x2-6x+8���ĶԳ�����x=-
=3��
��y=0����a��x2-6x+8��=0��
���x1=2��x2=4��
��x=0�����y=8a��
��� A��B��C������ֱ��ǣ�2��0������4��0������0��8a����
�ʴ�Ϊ��x=3����2��0������4��0����
��2����ͼ�٣��������߶Գ�����x��Ľ���ΪM����AM=1��
������ã�O��A=OA=2��
��O��A=2AM��
���O��AM=60�㣬
���OAC=��O��AC=60�㣬
��OC=2
����8a=2
��
��a=
��
��3������P�㣬ʹ���߶�PA��PB��PC��PD�ܹ���һ��ƽ���ı��Σ�
��ͼ�ڣ��ߵ�A��B����������x�ύ�㣬��P�������߶Գ����ϣ�
��PA=PB��
�൱PC=PDʱ���߶�PA��PB��PC��PD�ܹ���һ��ƽ���ı��Σ�
�ߵ�C�������ǣ�0��8a������D�������ǣ�3��-a����
��P�������ǣ�3��n����
��PC2=32+��n-8a��2��PD2=��n+a��2��
��PC=PD��PC2=PD2��
��32+��n-8a��2=��n+a��2��
�����ã�7a2-2na+1=0��
���n=
=
=
��
��n=
ʱ����P��3��
��ʹ���߶�PA��PB��PC��PD�ij�����һ��ƽ���ı��ε������߳���Ӧ��ȣ�
 �⣺��1�����κ���y=a��x2-6x+8���ĶԳ�����x=-
�⣺��1�����κ���y=a��x2-6x+8���ĶԳ�����x=-| -6a |
| 2a |
��y=0����a��x2-6x+8��=0��
���x1=2��x2=4��
��x=0�����y=8a��
��� A��B��C������ֱ��ǣ�2��0������4��0������0��8a����
�ʴ�Ϊ��x=3����2��0������4��0����
��2����ͼ�٣��������߶Գ�����x��Ľ���ΪM����AM=1��
������ã�O��A=OA=2��
��O��A=2AM��
���O��AM=60�㣬
���OAC=��O��AC=60�㣬
��OC=2
| 3 |
| 3 |
��a=
| ||
| 4 |
��3������P�㣬ʹ���߶�PA��PB��PC��PD�ܹ���һ��ƽ���ı��Σ�

��ͼ�ڣ��ߵ�A��B����������x�ύ�㣬��P�������߶Գ����ϣ�
��PA=PB��
�൱PC=PDʱ���߶�PA��PB��PC��PD�ܹ���һ��ƽ���ı��Σ�
�ߵ�C�������ǣ�0��8a������D�������ǣ�3��-a����
��P�������ǣ�3��n����
��PC2=32+��n-8a��2��PD2=��n+a��2��
��PC=PD��PC2=PD2��
��32+��n-8a��2=��n+a��2��
�����ã�7a2-2na+1=0��
���n=
| 7a2+1 |
| 2a |
7��(
| ||||
2��
|
11
| ||
| 8 |
��n=
11
| ||
| 8 |
11
| ||
| 8 |
���������⿼���˶��κ������ۺ��⣬�����˶��κ�����ͼ�������ʣ�ֱ�������ε����ʣ��Ѷ��κ���ͼ�������ʺ�ƽ���ı��ε��ж������ǽ���ؼ���

��ϰ��ϵ�д�
�����Ŀ
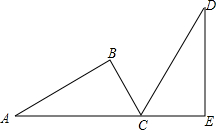 ��ͼ���ڡ�ABC�У���ACB=90�㣬��A=30�㣬�ѡ�ABC�Ƶ�C��תһ���ǶȺ�õ���DEC����A��C��E��ͬһֱ���ϣ��������ת�Ƕ�Ϊ��������
��ͼ���ڡ�ABC�У���ACB=90�㣬��A=30�㣬�ѡ�ABC�Ƶ�C��תһ���ǶȺ�õ���DEC����A��C��E��ͬһֱ���ϣ��������ת�Ƕ�Ϊ��������| A��60�� | B��90�� |
| C��120�� | D��150�� |
 ��ͼ����ABDΪ�ȱ������Σ���BCA=60�㣮��֤��AC=BC+CD��
��ͼ����ABDΪ�ȱ������Σ���BCA=60�㣮��֤��AC=BC+CD��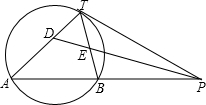 ��ͼ��PT�ǡ�O�����ߣ��е�ΪT��ֱ��PA���O����A��B���㣬��TPA��ƽ���߷ֱ�ֱ��TA��TB��D��E���㣮��֪PT=2��PB=
��ͼ��PT�ǡ�O�����ߣ��е�ΪT��ֱ��PA���O����A��B���㣬��TPA��ƽ���߷ֱ�ֱ��TA��TB��D��E���㣮��֪PT=2��PB=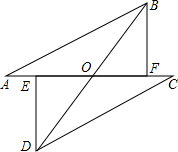 ��֪��ͼ���߶�AC��BD����O����AOBΪ�۽ǣ�AB=CD��BF��AC�ڵ�F��DE��AC�ڵ�E��AE=CF����֤��BD��EF����ƽ�֣�
��֪��ͼ���߶�AC��BD����O����AOBΪ�۽ǣ�AB=CD��BF��AC�ڵ�F��DE��AC�ڵ�E��AE=CF����֤��BD��EF����ƽ�֣�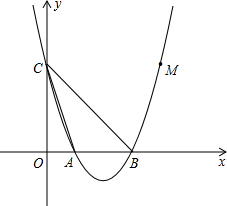 ��ͼ����֪������y=a��x-1����x-3����x��������ҷֱ���A��B���㣬��y�ύ�ڵ�C���������߹���M��4��3��������AC��BC��
��ͼ����֪������y=a��x-1����x-3����x��������ҷֱ���A��B���㣬��y�ύ�ڵ�C���������߹���M��4��3��������AC��BC��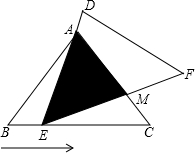 �ڡ�ABC�У���֪AB=AC=5��BC=6���ҡ�ABC�ա�DEF������DEF���ABC�غ���һ�𣬡�ABC��������DEF�˶��������㣺��E�ڱ�BC����B��C�ķ����˶�����DEʼ�վ�����A��EF��AC����M�㣮
�ڡ�ABC�У���֪AB=AC=5��BC=6���ҡ�ABC�ա�DEF������DEF���ABC�غ���һ�𣬡�ABC��������DEF�˶��������㣺��E�ڱ�BC����B��C�ķ����˶�����DEʼ�վ�����A��EF��AC����M�㣮 ��ͼ����3��3�ķ������У�����AB��BC��CA����۲첢������1����2��������6��Ȼ��ش��������⣺
��ͼ����3��3�ķ������У�����AB��BC��CA����۲첢������1����2��������6��Ȼ��ش��������⣺