题目内容
在△ABC中，∠A=60°，AC=8
，AB=4
+9，⊙O与边AB、AC相切于E、F，若⊙O在变化过程中都是落在△ABC内（含相切时），则线段AE的最大值为 ．
| 3 |
| 3 |
考点：切线的性质
专题：
分析：根据题意判断出当⊙O与△ABC的三边均相切时，线段AE的长度最大；运用余弦定理求出BC的长度；
利用切线的性质定理列出方程组；解关于x、y、z的方程组即可解决问题．
利用切线的性质定理列出方程组；解关于x、y、z的方程组即可解决问题．
解答：解：如图，
当⊙O与边AB、AC、BC分别相切于E、F、D三点时，
线段AE的长最大；
由切线的性质定理得：
AE=AF（设为x），BD=BE（设为y），CD=CF（设为z），
∴x+y=4
+9 ①，x+z=8
②；
由余弦定理得：BC2=AB2+AC2-2AB•ACcos∠A
=(4
+9)2+(8
)2-2(4
+9)×8
×
=48+72
+81+64×3-32×3-72
=225，
∴BC=15；
∴y+z=15 ③；
联立①、②、③得：
；
由①+②+③得：x+y+z=6
+12 ④，
由④-③得：x=6
-3，
∴线段AE的最大值为6
-3，
故答案为：6
-3．
当⊙O与边AB、AC、BC分别相切于E、F、D三点时，
线段AE的长最大；
由切线的性质定理得：
AE=AF（设为x），BD=BE（设为y），CD=CF（设为z），
∴x+y=4
| 3 |
| 3 |
由余弦定理得：BC2=AB2+AC2-2AB•ACcos∠A
=(4
| 3 |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
=48+72
| 3 |
| 3 |
=225，
∴BC=15；
∴y+z=15 ③；
联立①、②、③得：
|
由①+②+③得：x+y+z=6
| 3 |
由④-③得：x=6
| 3 |
∴线段AE的最大值为6
| 3 |
故答案为：6
| 3 |
点评：该题主要考查了切线的性质定理及其应用问题；解题的关键是：运用余弦定理求出BC的长度，运用切线的性质定理列出关于AE的方程组，解方程组．
练习册系列答案
相关题目
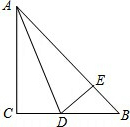如图所示，在等腰直角△ABC中∠C=90°，AD平分∠CAB交BC于D，DE⊥AB于E．若AB=10cm，则△DEB的周长为
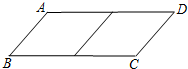邻边不相等的平行四边形纸片，剪去一个菱形，余下一个四边形，称为第一次操作；在余下的四边形纸片中再剪去一个菱形，又剩下一个四边形，称为第二次操作；…依此类推，若第n次操作后，余下的四边形是菱形，则称原平行四边形为n阶准菱形．例如：如图，?ABCD中，若AB=1，BC=2，则?ABCD为1阶准菱形．
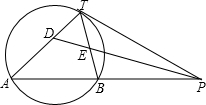如图，PT是⊙O的切线，切点为T，直线PA与⊙O交于A、B两点，∠TPA的平分线分别交直线TA、TB于D、E两点．已知PT=2，PB=