题目内容
19.适合于∠A=$\frac{1}{2}$$∠B=\frac{1}{3}$∠C的三角形是直角三角形.分析 由∠A=$\frac{1}{2}$$∠B=\frac{1}{3}$∠C可得到∠B、∠C与∠A间关系,根据三角形的内角和定理,求出∠B、∠C、∠A的度数,从而判断出三角形的形状.
解答 解:∵∠A=$\frac{1}{2}$$∠B=\frac{1}{3}$∠C,
∴∠B=2∠A,∠C=3∠A.
又∵∠A+∠B+∠C=180°,
即∠A+2∠A+3∠A=180°,
∴∠A=30°,∠B=60°,∠C=90°
故答案为:直角.
点评 本题考查了三角形的内角和定理,利用三角形的内角和是180°和∠B、∠C与∠A间关系,是解决本题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
9.说明命题“如果a,b,c是△ABC的三边,那么长为a2,b2,c2的三条线段能构成三角形”是假命题的反例可以是( )
| A. | a=2,b=2,c=3 | B. | a=2,b=2,c=2 | C. | a=2,b=2,c=4 | D. | a=3,b=4,c=4 |
 如图,四边形ABCD中,AD∥BC,AB⊥BC,点E在线段AB上,DE⊥CE.
如图,四边形ABCD中,AD∥BC,AB⊥BC,点E在线段AB上,DE⊥CE.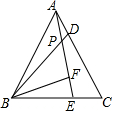 如图,在△ABC中,∠C=60°,AB=BC,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F,若BP=6,则PF的长为( )
如图,在△ABC中,∠C=60°,AB=BC,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F,若BP=6,则PF的长为( )