题目内容
4.已知2a=5,2b=10,2c=50,那么a,b,c之间满足的等量关系是a+b=c.分析 根据同底数幂的乘法可得2a•2b=50,进而可得a+b=c.
解答 解:∵2a=5,2b=10,
∴2a•2b=50,
2 a+b=50,
∵2c=50,
∴a+b=c,
故答案为:a+b=c.
点评 此题主要考查了同底数幂的乘法,关键是掌握同底数幂相乘,底数不变,指数相加.

练习册系列答案
相关题目
12.已知正方形ABCD的边长为1,E、F分别为BC、CD上的点,且满足BE=CF,则△AEF的面积的最小值是( )
| A. | $\frac{\sqrt{2}}{8}$ | B. | $\frac{\sqrt{3}}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{8}$ |
14.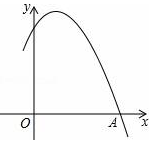 如图是二次函数y=ax2+bx+c图象的一部分,其图象的对称轴是直线x=1,且过点A(3,0),则下列结论正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,其图象的对称轴是直线x=1,且过点A(3,0),则下列结论正确的是( )
 如图是二次函数y=ax2+bx+c图象的一部分,其图象的对称轴是直线x=1,且过点A(3,0),则下列结论正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,其图象的对称轴是直线x=1,且过点A(3,0),则下列结论正确的是( )| A. | ac>0 | B. | 4a+2b+c<0 | C. | a-b+c>0 | D. | b2>4ac |
 在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上.
在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上.
 如图,四边形ABCD中,对角线AC⊥BD于点O,且AO=BO=4,CO=8,∠ADB=2∠ACB,则四边形ABCD的面积为42.
如图,四边形ABCD中,对角线AC⊥BD于点O,且AO=BO=4,CO=8,∠ADB=2∠ACB,则四边形ABCD的面积为42.