题目内容
8.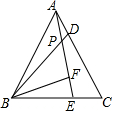 如图,在△ABC中,∠C=60°,AB=BC,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F,若BP=6,则PF的长为( )
如图,在△ABC中,∠C=60°,AB=BC,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F,若BP=6,则PF的长为( )| A. | 2 | B. | 3 | C. | 1 | D. | 6 |
分析 先证明△ABD≌△CAE,推出∠ABD=∠CAE,求出∠BPF=∠APD=60°,得出∠PBF=30°,根据含30度角的直角三角形性质求出即可.
解答 解:∵在△ABC中,∠C=60°,AB=BC,
∴△ABC是等边三角形,
∴AB=AC.
∴∠BAC=∠C.
在△ABD和△CAE中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠C}\\{AD=CE}\end{array}\right.$,
∴△ABD≌△CAE(SAS).
∴∠ABD=∠CAE.
∴∠APD=∠ABP+∠PAB=∠BAC=60°.
∴∠BPF=∠APD=60°.
∵∠BFP=90°,∠BPF=60°,
∴∠PBF=30°.
∴PF=$\frac{1}{2}$PB=3.
故选:B.
点评 本题考查了等边三角形性质,全等三角形的性质和判定,三角形外角性质,含30度角的直角三角形性质的应用,关键是求出∠PBF=30°.

练习册系列答案
相关题目
3.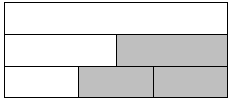 如图,三个大小相同的长方形拼在一起组成一个大长方形,把第二个长方形平均分成2份;再把第3个长方形平均分成3份,那么图中阴影部分是大长方形面积的( )
如图,三个大小相同的长方形拼在一起组成一个大长方形,把第二个长方形平均分成2份;再把第3个长方形平均分成3份,那么图中阴影部分是大长方形面积的( )
 如图,三个大小相同的长方形拼在一起组成一个大长方形,把第二个长方形平均分成2份;再把第3个长方形平均分成3份,那么图中阴影部分是大长方形面积的( )
如图,三个大小相同的长方形拼在一起组成一个大长方形,把第二个长方形平均分成2份;再把第3个长方形平均分成3份,那么图中阴影部分是大长方形面积的( )| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{18}$ |

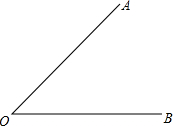 如图,下面是利用尺规作∠AOB的角平分线OC的作法,
如图,下面是利用尺规作∠AOB的角平分线OC的作法,