题目内容
8.已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.且△OCP与△PDA的面积比为1:4(1)如图1,已知折痕与边BC交于点O,连结AP、OP、OA.
①求证:△OCP∽△PDA;
②求边AB的长;
(2)如图2,连结AP、BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
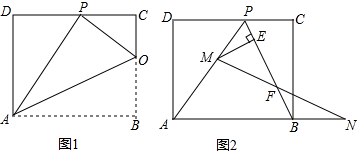
分析 (1)①只要证明∠PAD=∠CPO,由∠D=∠C=90°,即可证出△OCP∽△PDA;
②根据△OCP与△PDA的面积比为1:4,得出CP=$\frac{1}{2}$AD=4,设OP=x,则CO=8-x,由勾股定理得 x2=(8-x)2+42,求出x,最后根据AB=2OP即可求出边AB的长;
(2)作MQ∥AN,交PB于点Q,求出MP=MQ,BN=QM,得出MP=MQ,根据ME⊥PQ,得出EQ=$\frac{1}{2}$PQ,根据∠QMF=∠BNF,证出△MFQ≌△NFB,得出QF=$\frac{1}{2}$QB,
再求出EF=$\frac{1}{2}$PB,由(1)中的结论求出PB,即可判断.
解答 解:(1)①如图1中,∵四边形ABCD是矩形,
∴∠C=∠D=90°,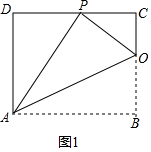
∴∠DPA+∠DAP=90°,
∵由折叠可得∠APO=∠B=90°,
∴∠DPA+∠CPO=90°,
∴∠DAP=∠CPO,
又∵∠D=∠C,
∴△OCP∽△PDA;
②如图1,∵△OCP与△PDA的面积比为1:4,
∴$\frac{OP}{PA}$=$\frac{CP}{DA}$=$\sqrt{\frac{1}{4}}$=$\frac{1}{2}$,
∴CP=$\frac{1}{2}$AD=4,
设OP=x,则CO=8-x,
在Rt△PCO中,∠C=90°,
由勾股定理得 x2=(8-x)2+42,
解得:x=5,
∴AB=AP=2OP=10,
∴边AB的长为10;
(2)结论:线段EF的长度不发生变化.EF=2$\sqrt{5}$.
理由:如图2中,作MQ∥AN,交PB于点Q,
∵AP=AB,MQ∥AN,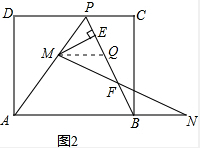
∴∠APB=∠ABP=∠MQP.
∴MP=MQ,
∵BN=PM,
∴BN=QM.
∵MP=MQ,ME⊥PQ,
∴EQ=$\frac{1}{2}$PQ.
∵MQ∥AN,
∴∠QMF=∠BNF,
在△MFQ和△NFB中,
$\left\{\begin{array}{l}{∠QFM=∠NFB}\\{∠QMF=∠BNF}\\{MQ=BN}\end{array}\right.$,
∴△MFQ≌△NFB(AAS),
∴QF=FB,
∴QF=$\frac{1}{2}$QB,
∴EF=EQ+QF=$\frac{1}{2}$PQ+$\frac{1}{2}$QB=$\frac{1}{2}$PB,
由(1)中的结论可得:PC=4,BC=8,∠C=90°,
∴PB=$\sqrt{{8}^{2}+{4}^{2}}$=4 $\sqrt{5}$,
∴EF=$\frac{1}{2}$PB=2 $\sqrt{5}$,
∴当点M、N在移动过程中,线段EF的长度不变,它的长度为2 $\sqrt{5}$.
点评 此题考查了相似形综合题、全等三角形的判定与性质、勾股定理、等腰三角形的性质,解题的关键是关键是学会添加辅助线,构造全等三角形解决问题,

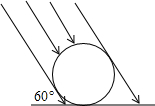 如图,太阳光线与地面成60°的角,照在地面的一只排球上,排球在地面的投影长是14$\sqrt{3}$cm,则排球的直径是( )
如图,太阳光线与地面成60°的角,照在地面的一只排球上,排球在地面的投影长是14$\sqrt{3}$cm,则排球的直径是( )| A. | 7cm | B. | 14cm | C. | 21cm | D. | 21$\sqrt{3}$cm |
| A. | 长度相等的弧是等弧 | B. | 三点确定一个圆 | ||
| C. | 圆周角是圆心角的一半 | D. | 直径所对的圆周角是直角 |
 在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上.
在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上.