题目内容
9.分解因式:(1)4a2-36
(2)(x-2y)2+8xy.
分析 (1)原式提取4,再利用平方差公式分解即可;
(2)原式整理后,利用完全平方公式分解即可.
解答 解:(1)原式=4(a2-9)=4(a+3)(a-3);
(2)原式=x2-4xy+4y2+8xy=x2+4xy+4y2=(x+2y)2.
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
4.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14.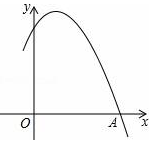 如图是二次函数y=ax2+bx+c图象的一部分,其图象的对称轴是直线x=1,且过点A(3,0),则下列结论正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,其图象的对称轴是直线x=1,且过点A(3,0),则下列结论正确的是( )
 如图是二次函数y=ax2+bx+c图象的一部分,其图象的对称轴是直线x=1,且过点A(3,0),则下列结论正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,其图象的对称轴是直线x=1,且过点A(3,0),则下列结论正确的是( )| A. | ac>0 | B. | 4a+2b+c<0 | C. | a-b+c>0 | D. | b2>4ac |
1.-2017的绝对值是( )
| A. | $\frac{1}{2017}$ | B. | ±2017 | C. | 2017 | D. | -2017 |
19.下列等式变形正确的是( )
| A. | 由a=b,得$\frac{a}{-4}$=$\frac{b}{-4}$ | B. | 由-3x=-3y,得x=-y | ||
| C. | 由$\frac{x}{4}$=1,得x=$\frac{1}{4}$ | D. | 由x=y,得$\frac{x}{a}$=$\frac{y}{a}$ |
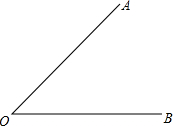 如图,下面是利用尺规作∠AOB的角平分线OC的作法,
如图,下面是利用尺规作∠AOB的角平分线OC的作法,