题目内容
9.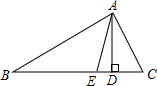 如图,在△ABC中,AD是BC边上的高,AE是∠BAC的角平分线,∠B=20°,∠C=60°.
如图,在△ABC中,AD是BC边上的高,AE是∠BAC的角平分线,∠B=20°,∠C=60°.(1)求∠EAD的度数;
(2)若其他条件不变,图形发生了变化,已知的两个角度数改为:
当∠B=30°,∠C=60°,则∠EAD=15°;
当∠B=50°,∠C=60°时,则∠EAD=5°;
当∠B=64°,∠C=78°时,则∠EAD=7°;
(3)若∠B<∠C,你能找到∠EAD与∠B和∠C之间的关系吗?请写出你发现的结论并说明理由.
分析 (1)根据三角形内角和定理求出∠BAC,根据三角形的高和角平分线的定义计算即可;
(2)同(1)的解法相同,计算即可;
(3)根据三角形内角和定理求出∠BAC,根据三角形的高和角平分线的定义计算即可.
解答 解:(1)∵∠B=20°,∠C=60°,
∴∠BAC=100°,
∵AE是∠BAC的角平分线,
∴∠EAC=50°,
∵AD⊥BC,∠C=60°,
∴∠DAC=30°,
∴∠EAD=20°,
(2)∠B=30°,∠C=60°,则∠EAD=15°
∠B=50°,∠C=60°时,则∠EAD=5°,
∠B=64°,∠C=78°时,则∠EAD=7°,
故答案为:15;5;7;
(3)∠EAD=$\frac{∠C-∠B}{2}$,
证明:∴∠BAC=180°-∠C-∠B,
∵AE是∠BAC的角平分线,
∴∠EAC=$\frac{180°-∠C-∠B}{2}$,
∵AD⊥BC,
∴∠DAC=90°-∠C,
∴∠EAD=$\frac{180°-∠C-∠B}{2}$-(90°-∠C)=$\frac{∠C-∠B}{2}$.
点评 本题考查的是三角形内角和定理、三角形的高、角平分线的定义,掌握相关定理、定义是解题的关键.

练习册系列答案
相关题目
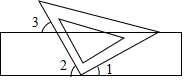 如图,一块直角三角尺的两个顶点分别在长方形的一组对边上,若∠1=30°,则∠3=60°.
如图,一块直角三角尺的两个顶点分别在长方形的一组对边上,若∠1=30°,则∠3=60°.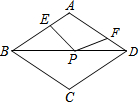 如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为3.
如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为3.