题目内容
17.等腰直角三角形中,若斜边为16,则直角边的长为8$\sqrt{2}$.分析 利用勾股定理,设直角边为a,则2a2=256求解即可.
解答 解:∵三角形为等腰直角三角形,
∴设两直角边为a,则a2+a2=162
解得a=8$\sqrt{2}$,
故答案为:8$\sqrt{2}$.
点评 本题考查了等腰直角三角形的性质,解题需注意根据等腰直角三角形的特点,利用勾股定理进行解答,还要注意,三角形的边长是正值.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
5.已知10x+y=3,10x-2y=5,则102x-y的值是( )
| A. | 3 | B. | 5 | C. | 15 | D. | $\frac{3}{5}$ |
12.若a>b,则下列不等式中错误的是( )
| A. | -$\frac{a}{5}<-\frac{b}{5}$ | B. | -2a>-2b | C. | a-2>b-2 | D. | -(-a)>-(-b) |
6.若凸n边形的每个外角都是36°,则从一个顶点出发引的对角线条数是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
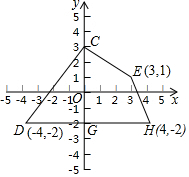 在平面直角坐标系中,四边形CDHE的位置如图所示,求四边形CDHE的面积.
在平面直角坐标系中,四边形CDHE的位置如图所示,求四边形CDHE的面积.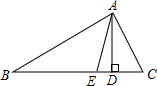 如图,在△ABC中,AD是BC边上的高,AE是∠BAC的角平分线,∠B=20°,∠C=60°.
如图,在△ABC中,AD是BC边上的高,AE是∠BAC的角平分线,∠B=20°,∠C=60°.