题目内容
9.化简:y[$\frac{x\sqrt{x}+x\sqrt{y}}{xy-{y}^{2}}-\frac{x+\sqrt{xy}+y}{x\sqrt{x}-y\sqrt{y}}$].分析 先算乘法,然后利用乘法公式进行化简,再计算减法即可.
解答 解:y[$\frac{x\sqrt{x}+x\sqrt{y}}{xy-{y}^{2}}-\frac{x+\sqrt{xy}+y}{x\sqrt{x}-y\sqrt{y}}$]
=$\frac{x(\sqrt{x}+\sqrt{y})}{x-y}$-$\frac{x+\sqrt{xy}+y}{(\sqrt{x}-\sqrt{y})(x+\sqrt{xy}+y)}$
=$\frac{x}{\sqrt{x}-\sqrt{y}}$-$\frac{1}{\sqrt{x}-\sqrt{y}}$
=$\frac{x-1}{\sqrt{x}-\sqrt{y}}$
=$\frac{x\sqrt{x}-x\sqrt{y}-\sqrt{x}+\sqrt{y}}{x-y}$.
点评 此题考查二次根式的混合运算,注意先化简,再进一步利用计算公式和计算方法计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
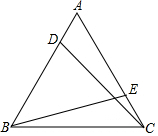 如图,在等边三角形ABC中,点D,E分别在边AB,AC上,且AD=CE,求证:CD=BE.
如图,在等边三角形ABC中,点D,E分别在边AB,AC上,且AD=CE,求证:CD=BE.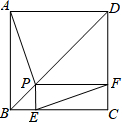 如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为$\sqrt{2}$;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为$\sqrt{2}$;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )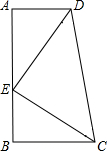 如图,在梯形ABCD中,AD∥BC,∠A=90°,点E在边AB上,AD=BE,AE=BC,由此可以知道△ADE旋转后能与△BEC重合,那么旋转中心是CD的中点.
如图,在梯形ABCD中,AD∥BC,∠A=90°,点E在边AB上,AD=BE,AE=BC,由此可以知道△ADE旋转后能与△BEC重合,那么旋转中心是CD的中点.