题目内容
14．
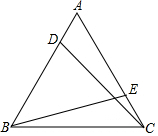如图，在等边三角形ABC中，点D，E分别在边AB，AC上，且AD=CE，求证：CD=BE．
分析 由三角形ABC为等边三角形，得到对应边相等，对应角相等，利用SAS得到三角形ACD与三角形CBE全等，利用全等三角形的对应边相等即可得证．
解答 证明：∵△ABC为等边三角形，
∴AC=BC，∠A=∠BCE=60°，
在△ACD和△CBE中，
$\left\{\begin{array}{l}{AD=CE}\\{∠A=∠BCE}\\{AC=CB}\end{array}\right.$，
∴△ACD≌△CBE（SAS），
则CD=BE．
点评 此题考查了全等三角形的判定与性质，以及等边三角形的性质，熟练掌握全等三角形的判定与性质是解本题的关键．
练习册系列答案
相关题目
4．
在图中，梯形的个数为（ ）
在图中，梯形的个数为（ ）| A． | 6 | B． | 9 | C． | 15 | D． | 27 |
已知：如图，D是△ABC的BC边的中点，DE⊥AC，DF⊥AB，垂足分别为E、F，且DE=DF．求证：△ABC是等腰三角形．
2．下列事件中，属于随机事件的是（ ）
| A． | （$\sqrt{a}$）2=a | B． | 若a＞b（ab≠0），则$\frac{1}{a}$＜$\frac{1}{b}$ | ||
| C． | |a|•|b|=|ab| | D． | 若m为整数，则（m+$\frac{1}{2}$）2+$\frac{7}{4}$是整数 |
19．某服装店公布以下好消息：为了感谢广大顾客的支持，即日起，在我店办会员卡同时享受以下两种优惠：
优惠一：
优惠二：
注：1-100是指购买服装的标价大于或等于1元且小于100元，其他类同．
若该店服装的标价都是正整数，请解决以下问题：
（1）在该店公布好消息的前、后，如果顾客都是充值1000元，在所买服装打折后的价格不超过会员卡内金额的前提下，可买到最贵的服装的标价相差了多少元？
（2）小红和小亮都在该店公布好消息之后办了会员卡，两人各买了一件标价高于300元的服装，小亮所买服装的标价比小红的高，但比较打折后的价格，小亮的低，求小亮买的服装的标价的范围．
优惠一：
| 充值金额（元） | 充值后卡内金额（元） | |
| 以前 | 即日起 | |
| 200 | 200 | 250 |
| 500 | 600 | 650 |
| 1000 | 1200 | 1400 |
| 购买服装的标价（元） | 折扣 | |
| 以前 | 即日起 | |
| 1-100 | 不打折 | 不打折 |
| 100-300 | 不打折 | 9折 |
| 300-400 | 9折 | 8折 |
| 不低于400 | 8折 | 7折 |
若该店服装的标价都是正整数，请解决以下问题：
（1）在该店公布好消息的前、后，如果顾客都是充值1000元，在所买服装打折后的价格不超过会员卡内金额的前提下，可买到最贵的服装的标价相差了多少元？
（2）小红和小亮都在该店公布好消息之后办了会员卡，两人各买了一件标价高于300元的服装，小亮所买服装的标价比小红的高，但比较打折后的价格，小亮的低，求小亮买的服装的标价的范围．
如图，在△ABC中，E，F分别是AB，BC的中点，M，N是AC的三等分点，EM，FN的延长线相交于点D．