题目内容
5. 如图,在Rt△ABC中,∠ABC=90°,AB=BC=$2\sqrt{2}$,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则BE的长是2$\sqrt{3}$+2.
如图,在Rt△ABC中,∠ABC=90°,AB=BC=$2\sqrt{2}$,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则BE的长是2$\sqrt{3}$+2.
分析 首先考虑到BE所在的三角形并不是特殊三角形,所以猜想到要求BE,可能需要构造直角三角形.由旋转的性质可知,AC=AE,∠CAE=60°,故△ACE是等边三角形,可证明△ABE与△CBE全等,可得到∠ABE=45°,∠AEB=30°,再证△AFB和△AFE是直角三角形,然后在根据勾股定理求解
解答 解:连结CE,设BE与AC相交于点F,如下图所示,
∵Rt△ABC中,AB=BC,∠ABC=90°
∴∠BCA=∠BAC=45°
∵Rt△ABC绕点A逆时针旋转60°与Rt△ADE重合,
∴∠BAC=∠DAE=45°,AC=AE
又∵旋转角为60°
∴∠BAD=∠CAE=60°,
∴△ACE是等边三角形
∴AC=CE=AE=4
在△ABE与△CBE中,$\left\{\begin{array}{l}{BA=BC}\\{AE=CE}\\{BE=BE}\end{array}\right.$
∴△ABE≌△CBE (SSS)
∴∠ABE=∠CBE=45°,∠CEB=∠AEB=30°
∴在△ABF中,∠BFA=180°-45°-45°=90°
∴∠AFB=∠AFE=90°
在Rt△ABF中,由勾股定理得,
BF=AF=$\sqrt{(\frac{AB}{2})^{2}}$=2
又在Rt△AFE中,∠AEF=30,°∠AFE=90°
FE=$\sqrt{3}$AF=2$\sqrt{3}$
∴BE=BF+FE=2+2$\sqrt{3}$
故,本题的答案是:2+2$\sqrt{3}$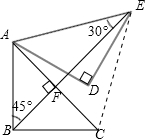
点评 此题是旋转性质题,解决此题,关键是思路要明确:“构造”直角三角形.在熟练掌握旋转的性质的基础上,还要应用全等的判定及性质,直角三角形的判定及勾股定理的应用

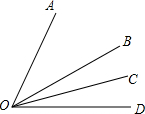 如图,OB平分∠AOD,OC平分∠BOD,∠AOC=45°,则∠BOC=( )
如图,OB平分∠AOD,OC平分∠BOD,∠AOC=45°,则∠BOC=( )| A. | 5° | B. | 10° | C. | 15° | D. | 20° |
 如图,菱形ABCD的一边中点M到对角线交点O的距离为5cm,则菱形ABCD的周长为( )
如图,菱形ABCD的一边中点M到对角线交点O的距离为5cm,则菱形ABCD的周长为( )| A. | 5 cm | B. | 10 cm | C. | 20 cm | D. | 40 cm |
①内错角相等;
②对顶角相等;
③对于任意实数x,代数式x2-6x+10总是正数;
④若三条线段a、b、c满足a+b>c,则三条线段a、b、c一定能组成三角形.
其中正确命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
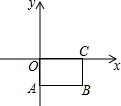 已知,矩形OABC按如图所示的方式建立在平面直角坐标系总,AB=4,BC=2,则点B的坐标为( )
已知,矩形OABC按如图所示的方式建立在平面直角坐标系总,AB=4,BC=2,则点B的坐标为( )| A. | (4,2) | B. | (-2,4) | C. | (4,-2) | D. | (-4,2) |
 完成下面的证明(在下面的括号内填上相应的结论或推理的依据):
完成下面的证明(在下面的括号内填上相应的结论或推理的依据):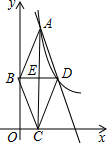 如图,点A是反比例函数y=$\frac{8}{x}$(x>0)的图象上的一个动点,AC⊥x轴于点C;E是线段AC的中点,过点E作AC的垂线,与y轴和反比例函数的图象分别交于点B、D两点;连结AB、BC、CD、DA.设点A的横坐标为m.
如图,点A是反比例函数y=$\frac{8}{x}$(x>0)的图象上的一个动点,AC⊥x轴于点C;E是线段AC的中点,过点E作AC的垂线,与y轴和反比例函数的图象分别交于点B、D两点;连结AB、BC、CD、DA.设点A的横坐标为m.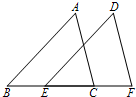 如图,△DEF是将△ABC沿射线BC的方向平移后得到的.若BC=5,EC=3,则CF的长为( )
如图,△DEF是将△ABC沿射线BC的方向平移后得到的.若BC=5,EC=3,则CF的长为( )