题目内容
15. 完成下面的证明(在下面的括号内填上相应的结论或推理的依据):
完成下面的证明(在下面的括号内填上相应的结论或推理的依据):如图,∠BED=∠B+∠D.
求证:AB∥CD.
证明:过点E作EF∥AB(平行公理).
∵EF∥AB(已作),
∴∠BEF=∠B(两直线平行,内错角相等).
∵∠BED=∠B+∠D(已知),
又∵∠BED=∠BEF+∠FED,
∴∠FED=∠D(等量代换).
∴EF∥CD(内错角相等,两直线平行).
∴AB∥CD(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
分析 先作出平行线,得出结论∠BEF=∠B,结合已知条件再判断∠FED=∠D即可.
解答 证明:过点E作EF∥AB.
∵EF∥AB,
∴∠BEF=∠B( 两直线平行,内错角相等).
∵∠BED=∠B+∠D,
又∵∠BED=∠BEF+∠FED,
∴∠FED=∠D.
∴EF∥CD(内错角相等,两直线平行).
∴AB∥CD(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
故答案为:两直线平行,内错角相等,∠D,内错角相等,两直线平行,如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
点评 此题是平行线的性质和判定,解本题的关键是熟练掌握平行线的性质和判定的同时要灵活运用.

练习册系列答案
相关题目
5. 如图,在△ABC中,AB=AC,BD平分∠ABC,若∠A=52°,则∠1的度数为( )
如图,在△ABC中,AB=AC,BD平分∠ABC,若∠A=52°,则∠1的度数为( )
 如图,在△ABC中,AB=AC,BD平分∠ABC,若∠A=52°,则∠1的度数为( )
如图,在△ABC中,AB=AC,BD平分∠ABC,若∠A=52°,则∠1的度数为( )| A. | 64° | B. | 78° | C. | 84° | D. | 88° |
10.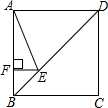 如图,正方形ABCD的边长为8,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
如图,正方形ABCD的边长为8,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
 如图,正方形ABCD的边长为8,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
如图,正方形ABCD的边长为8,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 8-4$\sqrt{2}$ | D. | 8$\sqrt{2}$-8 |
20. 如图,在四边形ABCD中,点E在BC上,连接AE,DE,∠BAE=∠EDC=47°,若AE∥CD,∠B=65°,则下列说法中不正确的是( )
如图,在四边形ABCD中,点E在BC上,连接AE,DE,∠BAE=∠EDC=47°,若AE∥CD,∠B=65°,则下列说法中不正确的是( )
 如图,在四边形ABCD中,点E在BC上,连接AE,DE,∠BAE=∠EDC=47°,若AE∥CD,∠B=65°,则下列说法中不正确的是( )
如图,在四边形ABCD中,点E在BC上,连接AE,DE,∠BAE=∠EDC=47°,若AE∥CD,∠B=65°,则下列说法中不正确的是( )| A. | ∠C=∠AEB | B. | AB∥DE | C. | ∠DEC=65° | D. | ∠AEB=58° |
 请在括号内加注理由或在横线上填入相关内容:
请在括号内加注理由或在横线上填入相关内容:



 如图,已知AD∥BC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E,试说明AB∥DC,把下面的说理过程补充完整.
如图,已知AD∥BC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E,试说明AB∥DC,把下面的说理过程补充完整. 如图,在Rt△ABC中,∠ABC=90°,AB=BC=$2\sqrt{2}$,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则BE的长是2$\sqrt{3}$+2.
如图,在Rt△ABC中,∠ABC=90°,AB=BC=$2\sqrt{2}$,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则BE的长是2$\sqrt{3}$+2.