题目内容
3.已知x1,x2,x3,x4,x5,x6方差是$\frac{5}{3}$,平均数是1.(1)求x12+x22+x32+x42+x52+x62的值;
(2)若加一个x7,平均数不变,求方差.
分析 (1)先由数据x1,x2,…x6的平均数为1,得出x1+x2+…+x6=1×6=6,再根据方差为$\frac{5}{3}$,得到S2=$\frac{1}{6}$[(x1-1)2+(x2-1)2+…+(x6-1)2]=$\frac{5}{3}$,利用完全平方公式求出$\frac{1}{6}$(x12+x22+…+x62-2×6+6)=$\frac{5}{3}$,进而求解即可;
(2)先由数据x1,x2,…x7的平均数为1,得出x1+x2+…+x7=1×7=7,而x1+x2+…+x6=6,所以x7=1;再根据$\frac{1}{6}$[(x1-1)2+(x2-1)2+…+(x6-1)2]=$\frac{5}{3}$,得出(x1-1)2+(x2-1)2+…+(x6-1)2=10,然后根据方差的计算公式即可求出这7个数据的方差.
解答 解:(1)∵数据x1,x2,…x6的平均数为1,
∴x1+x2+…+x6=1×6=6,
又∵方差为$\frac{5}{3}$,
∴S2=$\frac{1}{6}$[(x1-1)2+(x2-1)2+…+(x6-1)2]
=$\frac{1}{6}$[x12+x22+…+x62-2(x1+x2+…+x6)+6]
=$\frac{1}{6}$(x12+x22+…+x62-2×6+6)
=$\frac{1}{6}$(x12+x22+…+x62)-1=$\frac{5}{3}$,
∴x12+x22+…+x62=16;
(2)∵数据x1,x2,…x7的平均数为1,
∴x1+x2+…+x7=1×7=7,
∵x1+x2+…+x6=6,
∴x7=1,
∵$\frac{1}{6}$[(x1-1)2+(x2-1)2+…+(x6-1)2]=$\frac{5}{3}$,
∴(x1-1)2+(x2-1)2+…+(x6-1)2=10,
∴S2=$\frac{1}{7}$[(x1-1)2+(x2-1)2+…+(x7-1)2]
=$\frac{1}{7}$[10+(1-1)2]
=$\frac{10}{7}$.
点评 本题考查了平均数与方差的意义.平均数是指在一组数据中所有数据之和再除以数据的个数.一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差.

 如图,将纸片△ABC沿DE折叠,点A落在点F处.
如图,将纸片△ABC沿DE折叠,点A落在点F处. 在△ABC中,AD是∠BAC的角平分线,EF⊥BC,∠B>∠C,证明:∠FED=$\frac{1}{2}$(∠B-∠C)
在△ABC中,AD是∠BAC的角平分线,EF⊥BC,∠B>∠C,证明:∠FED=$\frac{1}{2}$(∠B-∠C)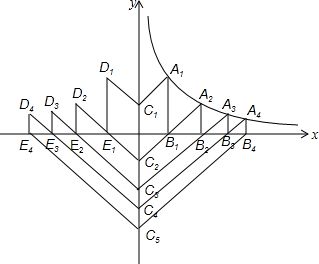 图中是某建筑公司的标识的设计原稿,该标志是由8个平行四边形组成,且关于y轴对称,点A1,A2,A3,A4在双曲线y=$\frac{k}{x}$(k≠0)的图象上,其中点A1(1,2),C1(0,1),则这个标志的面积为16.
图中是某建筑公司的标识的设计原稿,该标志是由8个平行四边形组成,且关于y轴对称,点A1,A2,A3,A4在双曲线y=$\frac{k}{x}$(k≠0)的图象上,其中点A1(1,2),C1(0,1),则这个标志的面积为16.