题目内容
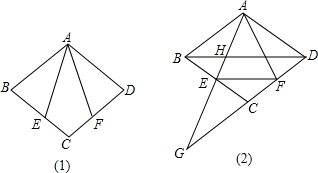
4.已知:如图(1),在平行四边形ABCD中,点E、F分别在BC、CD上,且AE=AF,∠AEC=∠AFC.(1)求证:四边形ABCD是菱形;
(2)如图(2),若AD=AF,延长AE、DC交于点G,求证:AF2=AG•DF;
(3)在第(2)小题的条件下,连接BD,交AG于点H,若HE=4,EG=12,求AH的长.
分析 (1)通过AAS证得△AEB≌△AFD,则其对应边相等:AB=AD,所以“邻边相等的平行四边形是菱形”;
(2)欲证明AF2=AG•DF,需要通过相似三角形△GAD∽△AFD的对应边成比例得到AD=AF,则AF2=AG•DF;
(3)根据菱形的性质和平行线分线段成比例得到:AH:HG=BH:HD,BH:HD=EH:AH,故AH:HG=EH:AH.把相关线段的长度代入来求AH的长度即可.
解答  (1)证明:如图1,∵四边形ABCD是平行四边形,
(1)证明:如图1,∵四边形ABCD是平行四边形,
∴∠B=∠D.
∵∠AEC=∠AFC,∠AEC+∠AEB=∠AFC+∠AFD=180°,
∴∠AEB=∠AFD.
在△AEB和△AFD中,
$\left\{\begin{array}{l}{∠B=∠D}\\{∠AEB=∠AFD}\\{AE=AF}\end{array}\right.$,
∴△AEB≌△AFD(AAS)
∴AB=AD,
∴平行四边形ABCD是菱形;
(2)由(1)知,△AEB≌△AFD,则∠BAE=∠DAF.
如图2,∵四边形ABCD是平行四边形,
∴AB∥DG,
∴∠BAE=∠G,
∴∠G=∠DAF.
又∵∠ADF=∠GDA,
∴△GAD∽△AFD,
∴DA:DF=DG:DA,
∴DA2=DG•DF.
∵DG:DA=AG:FA,且AD=AF,
∴DG=AG.
又∵AD=AF,
∴AF2=AG•DF;
(3)如图2,在菱形ABCD中,∵AB∥DC,AD∥BC,
∴AH:HG=BH:HD,BH:HD=EH:AH,
∴AH:HG=EH:AH.
∵HE=4,EG=12,
∴AH:16=4:AH,
∴AH=8.
点评 本题考查了相似综合题.此题综合性比较强,其中涉及到了菱形的性质,平行线分线段成比例,相似三角形的判定与性质,解题时,需要弄清楚相似三角形的对应边与对应角,以防弄错.

| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内含 |
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
| A. | a-3<b-3 | B. | a-b>0 | C. | $\frac{1}{3}a>\frac{1}{3}$b | D. | -2a<-2b |
 如图,正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )
如图,正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )| A. | x<-2或x>2 | B. | x<-2或0<x<2 | C. | -2<x<0或0<x<2 | D. | -2<x<0或x>2 |
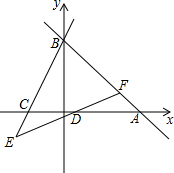 如图,直线y=-x+6与x轴交于点A,与y轴交于点B,C(-2,0),直线y=kx-k与x轴交于点D,交AB于F,交BC的延长线于E,若DE=DF,求k的值.
如图,直线y=-x+6与x轴交于点A,与y轴交于点B,C(-2,0),直线y=kx-k与x轴交于点D,交AB于F,交BC的延长线于E,若DE=DF,求k的值.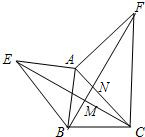 如图所示,已知AE=AB,AF=AC,EC=BF,求证:∠CMF=∠CAF.
如图所示,已知AE=AB,AF=AC,EC=BF,求证:∠CMF=∠CAF.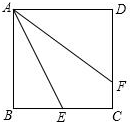 如图,正方形ABCD中,E为BC上的一点,DF=CF,DC+CE=AE,求证:AF平分∠DAE.
如图,正方形ABCD中,E为BC上的一点,DF=CF,DC+CE=AE,求证:AF平分∠DAE.