题目内容
18. 如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为( )
如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为( )| A. | 20 | B. | 22 | C. | 14 | D. | 16 |
分析 由在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M、N,作直线MN,可得MN是AB的垂直平分线,根据线段垂直平分线的性质,由△ADC的周长为8,即可得AC+BC=8,继而求得答案.
解答 解:根据题意得:MN是AB的垂直平分线,
∴AD=BD,
∵△ADC的周长为8,
∴AC+CD+AD=AC+CD+BD=AC+BC=8,
∵AB=6,
∴△ABC的周长为:AC+BC+AB=14.
故选C.
点评 此题考查了线段垂直平分线的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
3.某商家经销一种绿茶,用于装修门面已投资3000元.已知绿茶每千克成本50元,经研究发现销量y(kg)随销售单价x(元/kg)的变化而变化,具体变化规律如表所示:
设该绿茶的月销售利润为w(元)(销售利润=单价×销售量-成本)
(1)请根据上表,写出y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求w与x之间的函数关系式(不必写出自变量x的取值范围),并求出x为何值时,w的值最大?
(3)若在第一个月里,按使w获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于80元,要想在全部收回装修投资的基础上使第二个月的利润至少达到1700元,那么第二个月时里应该确定销售单价在什么范围内?
| 销售单价x(元/kg) | … | 70 | 75 | 80 | 85 | 90 | … |
| 月销售量y(kg) | … | 100 | 90 | 80 | 70 | 60 | … |
(1)请根据上表,写出y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求w与x之间的函数关系式(不必写出自变量x的取值范围),并求出x为何值时,w的值最大?
(3)若在第一个月里,按使w获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于80元,要想在全部收回装修投资的基础上使第二个月的利润至少达到1700元,那么第二个月时里应该确定销售单价在什么范围内?
10.当a>0时,下列关于幂的运算正确的是( )
| A. | a0=1 | B. | a-2=-a | C. | (-a)2=-a2 | D. | (ab)2=ab2 |
8. 若函数y=kx+b的图象如图所示,则关于x的不等式k(x+3)+b<0的解集为( )
若函数y=kx+b的图象如图所示,则关于x的不等式k(x+3)+b<0的解集为( )
 若函数y=kx+b的图象如图所示,则关于x的不等式k(x+3)+b<0的解集为( )
若函数y=kx+b的图象如图所示,则关于x的不等式k(x+3)+b<0的解集为( )| A. | x<2 | B. | x>2 | C. | x<-1 | D. | x>-1 |
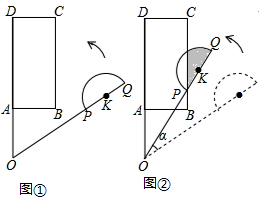 平面上,矩形ABCD与直径为QP的半圆K如图如图①摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针开始旋转,如图②,当点P恰好落在BC边上时,S阴影=$\frac{π}{24}$+$\frac{\sqrt{3}}{16}$.
平面上,矩形ABCD与直径为QP的半圆K如图如图①摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针开始旋转,如图②,当点P恰好落在BC边上时,S阴影=$\frac{π}{24}$+$\frac{\sqrt{3}}{16}$. 如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=4,DB=3,BC=9,则DE的长为$\frac{36}{7}$.
如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=4,DB=3,BC=9,则DE的长为$\frac{36}{7}$.