如图.在△ABC中.DE∥BC.分别交AB.AC于点D.E．若AD=4.DB=3.BC=9.则DE的长为$\frac{36}{7}$．题目和参考答案——青夏教育精英家教网—

题目内容

7．

如图，在△ABC中，DE∥BC，分别交AB，AC于点D，E．若AD=4，DB=3，BC=9，则DE的长为$\frac{36}{7}$．

分析求出AB，根据平行线得出△ADE∽△ABC，根据相似得出比例式，代入求出即可．

解答解：∵AD=4，DB=3，
∴AB=AD+DB=7，
∵DE∥BC，
∴△ADE∽△ABC，
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$，即$\frac{4}{7}$=$\frac{DE}{9}$，
则DE=$\frac{36}{7}$．
故答案为：$\frac{36}{7}$．

点评本题考查了相似三角形的性质和判定，关键是求出相似后得出比例式，题目比较典型，难度适中．

练习册系列答案

18．

如图，在△ABC中，分别以点A和点B为圆心，大于$\frac{1}{2}$AB的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD，若△ADC的周长为8，AB=6，则△ABC的周长为（　　）

15．如图是某几何体的三视图，其侧面积（　　）

2．如图，在矩形ABCD中，BC=1，∠CBD=60°，点E是AB边上一动点（不与点A，B重合），连接DE，过点D作DF⊥DE交BC的延长线于点F，连接EF交CD于点G．

（1）求证：△ADE∽△CDF；
（2）求∠DEF的度数；
（3）设BE的长为x，△BEF的面积为y．
①求y关于x的函数关系式，并求出当x为何值时，y有最大值；
②当y为最大值时，连接BG，请判断此时四边形BGDE的形状，并说明理由．

12．

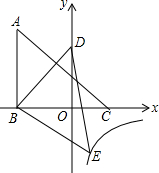如图，△ABC的三个顶点的坐标分别为A（-3，5），B（-3，0），C（2，0），将△ABC绕点B顺时针旋转一定的角度后得到△DBE，且使点D落在y轴上，与此同时顶点E恰好落在y=$\frac{k}{x}$的图象上，则k的值为（　　）

19．观察下列图形规律：当n=（　　）时，图形“•”的个数和“△”的个数相等

16．

如图，在Rt△ABC中，∠C=90°，∠B=30°，将Rt△ABC绕点A按顺时针方向旋转到△AB₁C₁的位置，使得点C、A、B₁在同一条直线上，那么旋转角最小为（　　）

5．

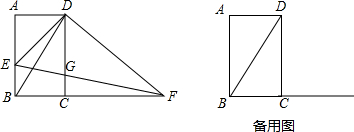
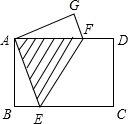如图，矩形纸片ABCD中，AB=3cm，BC=4cm，现将A、C重合，使纸片折叠压平，设折痕为EF，试确定重叠部分的△AEF的面积是$\frac{25}{16}$．

试题分类