题目内容
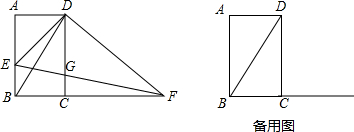
13.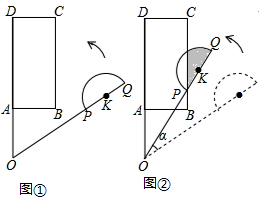 平面上,矩形ABCD与直径为QP的半圆K如图如图①摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针开始旋转,如图②,当点P恰好落在BC边上时,S阴影=$\frac{π}{24}$+$\frac{\sqrt{3}}{16}$.
平面上,矩形ABCD与直径为QP的半圆K如图如图①摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针开始旋转,如图②,当点P恰好落在BC边上时,S阴影=$\frac{π}{24}$+$\frac{\sqrt{3}}{16}$.
分析 首先设半圆K与PC交点为R,连接RK,过点P作PH⊥AD于点H,过点R作RE⊥KQ于点E,则可求得∠RKQ的度数,于是求得答案.
解答 解:如图所示: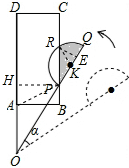 设半圆K与PC交点为R,连接RK,过点P作PH⊥AD于点H
设半圆K与PC交点为R,连接RK,过点P作PH⊥AD于点H
过点R作RE⊥KQ于点E,在Rt△OPH中,PH=AB=1,OP=2,
∴∠POH=30°,
∴α=60°-30°=30°,
∵AD∥BC,
∴∠RPO=∠POH=30°,
∴∠RKQ=2×30°=60°,
∴S扇形KRQ=$\frac{60π×(\frac{1}{2})^{2}}{360}$=$\frac{π}{24}$,
在Rt△RKE中,RE=RK•sin60°=$\frac{\sqrt{3}}{4}$,
∴S△PRK=$\frac{1}{2}$×$\frac{1}{2}$×$\frac{\sqrt{3}}{4}$=$\frac{\sqrt{3}}{16}$,
∴S阴影=$\frac{π}{24}$+$\frac{\sqrt{3}}{16}$;
故答案为:$\frac{π}{24}$+$\frac{\sqrt{3}}{16}$.
点评 本题考查了矩形的性质,直线与圆的位置关系,勾股定理以及锐角三角函数的知识.注意根据题意正确的画出图形是解题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
18. 如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为( )
如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为( )
 如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为( )
如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为( )| A. | 20 | B. | 22 | C. | 14 | D. | 16 |
5.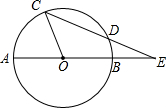 如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=87°,则∠E等于( )
如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=87°,则∠E等于( )
 如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=87°,则∠E等于( )
如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=87°,则∠E等于( )| A. | 42° | B. | 29° | C. | 21° | D. | 20° |
3. 如图,已知圆心角∠BOC=100°,则圆周角∠BAC的大小是( )
如图,已知圆心角∠BOC=100°,则圆周角∠BAC的大小是( )
 如图,已知圆心角∠BOC=100°,则圆周角∠BAC的大小是( )
如图,已知圆心角∠BOC=100°,则圆周角∠BAC的大小是( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |