题目内容
6. 如图,已知抛物线y=x2+bx+c经过A(0,-1)、B(4,-3)两点.
如图,已知抛物线y=x2+bx+c经过A(0,-1)、B(4,-3)两点.(1)求抛物线的解析式;
(2)求tan∠ABO的值;
(3)过点B作BC⊥x轴,垂足为点C,点M是抛物线上一点,直线MN平行于y轴交直线AB于点N,如果M、N、B、C为顶点的四边形是平行四边形,求点N的坐标.
分析 (1)将A(-1,0)、B(4,5)分别代入y=x2+bx+c,求出b和c的值即可;
(2)过点B作BC⊥x轴,垂足为C,过点A作AH⊥OB,垂足为点H,根据三角函数可求出AH的长,进一步得到BH的长,进而得到在Rt△ABH中,tan∠ABO的值;
(3)根据待定系数法可求直线AB的解析式,设点M的坐标为(m,m2-$\frac{9}{2}$m-1),点N坐标为(m,-$\frac{1}{2}$m-1),再分两种情况:m2-4m=3或-m2+4m=3,进行讨论求出符合题意的点N的坐标即可.
解答 解:(1)将A(0,-1)、B(4,-3)分别代入y=x2+bx+c,
得$\left\{\begin{array}{l}c=-1\\ 16+4b+c=-3\end{array}\right.$,
解得b=-$\frac{9}{2}$,c=-1.
所以抛物线的解析式为y=x2-$\frac{9}{2}$x-1;
(2)过点B作BC⊥x轴,垂足为C,过点A作AH⊥OB,垂足为点H,
在Rt△AOH中,OA=1,sin∠AOH=sin∠OBC=$\frac{4}{5}$,
∴AH=OA•sin∠AOH=$\frac{4}{5}$,
∴OH=$\frac{3}{5}$,BH=OB-OH=$\frac{22}{5}$,
在Rt△ABH中,tan∠ABO=$\frac{AH}{BH}$=$\frac{4}{5}$÷$\frac{22}{5}$=$\frac{2}{11}$;
(3)设直线AB的解析式为y=kx+b,
则$\left\{\begin{array}{l}{b=-1}\\{kx+b=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=-1}\end{array}\right.$.
故直线AB的解析式为y=-$\frac{1}{2}$x-1,
设点M的坐标为(m,m2-$\frac{9}{2}$m-1),点N坐标为(m,-$\frac{1}{2}$m-1),
那么MN=|(m2-$\frac{9}{2}$m-1)-(-$\frac{1}{2}$m-1)|=|m2-4m|,
∵M、N、B、C为顶点的四边形是平行四边形,
∴MN=BC=3
解方程m2-4m=3得m=2±$\sqrt{7}$;
解方程-m2+4m=3得m=1或m=3;
所以符合题意的点N有4个,(2-$\sqrt{7}$,$\frac{\sqrt{7}}{2}$-2),(2+$\sqrt{7}$,-$\frac{\sqrt{7}}{2}$-2),(1,-$\frac{3}{2}$),(3,-$\frac{5}{2}$).
点评 本题考查了二次函数综合题.其中涉及到的知识点有待定系数法求二次函数的解析式,平行四边形的判定和性质,三角函数,解一元二次方程以及抛物线的性质,解答(3)题时要分类讨论.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O的切线,切点为B,连结AC交⊙O于D,∠C=38°.点E在AB右侧的半圆上运动(不与A、B重合),则∠AED的大小是( )
如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O的切线,切点为B,连结AC交⊙O于D,∠C=38°.点E在AB右侧的半圆上运动(不与A、B重合),则∠AED的大小是( )| A. | 62° | B. | 52° | C. | 38° | D. | 28° |
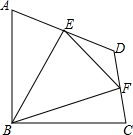 如图,在四边形ABCD中,∠ABC=90°,AB=BC=2$\sqrt{2}$,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( )
如图,在四边形ABCD中,∠ABC=90°,AB=BC=2$\sqrt{2}$,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( )| A. | 2 | B. | $\frac{9}{4}$ | C. | $\frac{5}{2}$ | D. | 3 |
| A. | 1.4(1+x)=4.5 | B. | 1.4(1+2x)=4.5 | ||
| C. | 1.4(1+x)2=4.5 | D. | 1.4(1+x)+1.4(1+x)2=4.5 |
| A. | a | B. | 2a | C. | 8a | D. | -8a |
| A. | $-\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | 0 | D. | 3 |
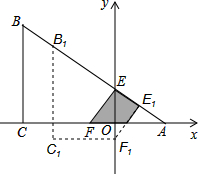 如图,有一张直角三角形纸片ABC,∠ACB=90°,∠B=60°,BC=3,直角边AC在x轴上,B点在第二象限,A($\sqrt{3}$,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在的直线上,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA方向平行移动,至B点到达A点停止(记平移后的四边形为B1C1F1E1).在平移过程中,设平移的距离BB1=x,四边形B1C1F1E1与△AEF重叠的面积为S.
如图,有一张直角三角形纸片ABC,∠ACB=90°,∠B=60°,BC=3,直角边AC在x轴上,B点在第二象限,A($\sqrt{3}$,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在的直线上,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA方向平行移动,至B点到达A点停止(记平移后的四边形为B1C1F1E1).在平移过程中,设平移的距离BB1=x,四边形B1C1F1E1与△AEF重叠的面积为S.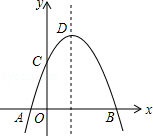 如图,抛物线y=-x2+2x+m+1交x轴与点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:
如图,抛物线y=-x2+2x+m+1交x轴与点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题: