题目内容
14.先化简,再求值:$\frac{{x}^{2}-8x+16}{{x}^{2}+2x}$÷(x-2-$\frac{12}{x+2}$)-$\frac{1}{x+4}$,其中x为方程5x+1=2(x-1)的解.分析 先根据分式混合运算的法则把原式进行化简,再求出x的值,代入原式进行计算即可.
解答 解:原式=$\frac{(x-4)^{2}}{x(x+2)}$÷$\frac{{x}^{2}-16}{x+2}$-$\frac{1}{x+4}$
=$\frac{(x-4)^{2}}{x(x+2)}$•$\frac{x+2}{(x+4)(x-4)}$-$\frac{1}{x+4}$
=$\frac{x-4}{x(x+4)}$-$\frac{x}{x(x+4)}$
=-$\frac{4}{x(x+4)}$,
由方程5x+1=2(x-1),解得:x=-1,
∴当x=-1时,原式=-$\frac{4}{-1×(-1+4)}$=$\frac{4}{3}$.
点评 本题主要考查分式的化简求值及解方程的能力,熟练运用分式的运算法则与分式的性质化简原式是解题的关键.

练习册系列答案
相关题目
2.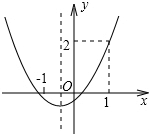 已知抛物线y=ax2+bx+c的图象如图所示,则下列结论中正确是( )
已知抛物线y=ax2+bx+c的图象如图所示,则下列结论中正确是( )
 已知抛物线y=ax2+bx+c的图象如图所示,则下列结论中正确是( )
已知抛物线y=ax2+bx+c的图象如图所示,则下列结论中正确是( )| A. | a+b+c>2 | B. | 2a-b<0 | C. | b<1 | D. | 3a+c>2 |
9.-16的倒数是( )
| A. | -$\frac{1}{16}$ | B. | $\frac{1}{16}$ | C. | -16 | D. | 16 |
4.在Rt△ABC中,∠C=90°,sinA=$\frac{4}{5}$,AC=6cm,则BC的长度为( )
| A. | 6cm | B. | 7cm | C. | 8cm | D. | 9cm |
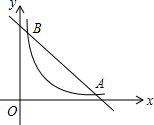 如图,在直角坐标系中,直线y=6-x与双曲线$y=\frac{4}{x}$ (x>0)的图象相交于A、B,设点A的坐标为(m,n),那么以m为长,n为宽的矩形的面积和周长分别为4,12.
如图,在直角坐标系中,直线y=6-x与双曲线$y=\frac{4}{x}$ (x>0)的图象相交于A、B,设点A的坐标为(m,n),那么以m为长,n为宽的矩形的面积和周长分别为4,12.
 将如图所示的Rt△ABC绕直角边AB旋转一周,则所得几何体的主视图为( )
将如图所示的Rt△ABC绕直角边AB旋转一周,则所得几何体的主视图为( )



 如图,已知抛物线y=x2+bx+c经过A(0,-1)、B(4,-3)两点.
如图,已知抛物线y=x2+bx+c经过A(0,-1)、B(4,-3)两点.