��Ŀ����
17��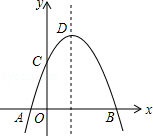 ��ͼ��������y=-x2+2x+m+1��x�����A��a��0����B��b��0������y���ڵ�C�������ߵĶ���ΪD�������ĸ����⣺
��ͼ��������y=-x2+2x+m+1��x�����A��a��0����B��b��0������y���ڵ�C�������ߵĶ���ΪD�������ĸ����⣺�ٵ�x��0ʱ��y��0��
����a=-1����b=4��
����������������P��x1��y1����Q��x2��y2������x1��1��x2����x1+x2��2����y1��y2��
�ܵ�C���������߶Գ���ĶԳƵ�ΪE����G��F�ֱ���x���y���ϣ���m=2ʱ���ı���EDFG�ܳ�����СֵΪ6��
���������������ǣ�������
| A�� | �� | B�� | �� | C�� | �� | D�� | �� |
���� ������������x���Ϸ�����Ӧ���Ա����ķ�Χ�ɶԢٽ����жϣ�����������ߵĶԳ��ᣬȻ�����������ߵĶԳ��ԿɶԢڽ����жϣ�����������ߵĶԳ��᷽�̣�Ȼ��Ƚϵ�P��Q���Գ���ľ����С������ݶ��κ����Ĵ�С�ɶԢ۽����жϣ������D���E�����꣬����D�����y��ĶԳƵ�D�䣨-1��4����E�����x��ĶԳƵ�E�䣨2��-3��������D��E��ֱ�x���y����G��F�㣬��ͼ����������֮���߶���̿��жϴ�ʱDF+FG+GE��ֵ��С�������ı���EDFG�ܳ�����С��Ȼ�����ù��ɶ��������DE��D��E�䣬��ɶԢܽ����жϣ�
��� �⣺��a��x��bʱ��y��0�����Ԣٴ���
�����ߵĶԳ���Ϊֱ��x=-$\frac{2}{2����-1��}$=1������A������Ϊ��-1��0������B��3��0�������Ԣڴ���
�����ߵĶԳ���Ϊֱ��x=1����x1��1��x2�����P��Q�ڶԳ�������ԣ���Ϊx1+x2��2�����Ե�Q��Գ����Զ������y1��y2�����Ԣ���ȷ��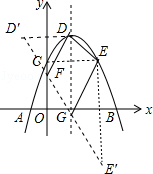 ��m=2����y=-x2+2x+3=-��x-1��2+4����D��1��4������x=0ʱ��y=-x2+2x+3=3����C��0��3����C����ڶԳ���ĶԳƵ�E������Ϊ��2��3������D�����y��ĶԳƵ�D�䣨-1��4����E�����x��ĶԳƵ�E�䣨2��-3��������D��E��ֱ�x���y����G��F�㣬��ͼ��
��m=2����y=-x2+2x+3=-��x-1��2+4����D��1��4������x=0ʱ��y=-x2+2x+3=3����C��0��3����C����ڶԳ���ĶԳƵ�E������Ϊ��2��3������D�����y��ĶԳƵ�D�䣨-1��4����E�����x��ĶԳƵ�E�䣨2��-3��������D��E��ֱ�x���y����G��F�㣬��ͼ��
����DF+FG+GE=D��F+FG+GE��=D��E�䣬��ʱDF+FG+GE��ֵ��С�������ı���EDFG�ܳ�����С����Сֵ=$\sqrt{{1}^{2}+��4-3��^{2}}$+$\sqrt{��-1-2��^{2}+��4+3��^{2}}$=$\sqrt{2}$+$\sqrt{58}$�����Ԣܴ���
��ѡC��
���� ���⿼���������붨�����ж�һ���������䣬�������⣮�������ⶼ��������ͽ�����������ɣ��ж�ǰ��3��������ٵĹؼ�����Ϥ���κ��������ʣ��ж����һ���������ٵĹؼ����������·���Ľ��������


| A�� | 56 | B�� | 63 | C�� | 70 | D�� | 77 |
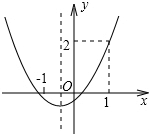 ��֪������y=ax2+bx+c��ͼ����ͼ��ʾ�������н�������ȷ�ǣ�������
��֪������y=ax2+bx+c��ͼ����ͼ��ʾ�������н�������ȷ�ǣ�������| A�� | a+b+c��2 | B�� | 2a-b��0 | C�� | b��1 | D�� | 3a+c��2 |
| A�� | -$\frac{1}{16}$ | B�� | $\frac{1}{16}$ | C�� | -16 | D�� | 16 |
| A�� | ת��˼�� | B�� | ����˼�� | C�� | ����˼�� | D�� | ���ν��˼�� |
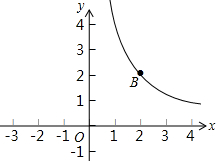 ��ƽ��ֱ������ϵxOy�У�����y=$\frac{k}{x}$��k��0��x��0����ͼ����ͼ��ʾ����֪��ͼ��A��m��n����B��2��2�����㣮����B��BD��y���ڵ�D������A��AC��x���ڵ�C��AC��BD���ڵ�F��һ�κ���y=ax+b��a��0����ͼ����A��D����x��ĸ����ύ�ڵ�E��
��ƽ��ֱ������ϵxOy�У�����y=$\frac{k}{x}$��k��0��x��0����ͼ����ͼ��ʾ����֪��ͼ��A��m��n����B��2��2�����㣮����B��BD��y���ڵ�D������A��AC��x���ڵ�C��AC��BD���ڵ�F��һ�κ���y=ax+b��a��0����ͼ����A��D����x��ĸ����ύ�ڵ�E��
 ��ͼ��������ֽƬABCD�۵���ʹ��A���C�غϣ��ۺ�ΪEF��EF��AC���ڵ�O���ֱ�����AE��CF����AB=$\sqrt{3}$����DCF=30�㣬��EF�ij�Ϊ2��
��ͼ��������ֽƬABCD�۵���ʹ��A���C�غϣ��ۺ�ΪEF��EF��AC���ڵ�O���ֱ�����AE��CF����AB=$\sqrt{3}$����DCF=30�㣬��EF�ij�Ϊ2�� ��ͼ����֪������y=x2+bx+c����A��0��-1����B��4��-3�����㣮
��ͼ����֪������y=x2+bx+c����A��0��-1����B��4��-3�����㣮