题目内容
11.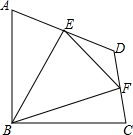 如图,在四边形ABCD中,∠ABC=90°,AB=BC=2$\sqrt{2}$,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( )
如图,在四边形ABCD中,∠ABC=90°,AB=BC=2$\sqrt{2}$,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( )| A. | 2 | B. | $\frac{9}{4}$ | C. | $\frac{5}{2}$ | D. | 3 |
分析 连接AC,过B作EF的垂线,利用勾股定理可得AC,易得△ABC的面积,可得BG和△ADC的面积,三角形ABC与三角形ACD同底,利用面积比可得它们高的比,而GH又是△ACD以AC为底的高的一半,可得GH,易得BH,由中位线的性质可得EF的长,利用三角形的面积公式可得结果.
解答 解:连接AC,过B作EF的垂线交AC于点G,交EF于点H,
∵∠ABC=90°,AB=BC=2$\sqrt{2}$,
∴AC=$\sqrt{{AB}^{2}{+BC}^{2}}$=$\sqrt{{(2\sqrt{2})}^{2}{+(2\sqrt{2})}^{2}}$=4,
∵△ABC为等腰三角形,BH⊥AC,
∴△ABG,△BCG为等腰直角三角形,
∴AG=BG=2
∵S△ABC=$\frac{1}{2}$•AB•BC=$\frac{1}{2}$×2$\sqrt{2}$×2$\sqrt{2}$=4,
∴S△ADC=2,
∵$\frac{{S}_{△ABC}}{{S}_{△ACD}}$=2,
∵△DEF∽△DAC,
∴GH=$\frac{1}{4}$BG=$\frac{1}{2}$,
∴BH=$\frac{5}{2}$,
又∵EF=$\frac{1}{2}$AC=2,
∴S△BEF=$\frac{1}{2}$•EF•BH=$\frac{1}{2}$×2×$\frac{5}{2}$=$\frac{5}{2}$,
故选C.
方法二:S△BEF=S四边形ABCD-S△ABE-S△BCF-S△FED,
易知S△ABE+S△BCF=$\frac{1}{2}$S四边形ABCD=3,S△EDF=$\frac{1}{2}$,
∴S△BEF=S四边形ABCD-S△ABE-S△BCF-S△FED=6-3-$\frac{1}{2}$=$\frac{5}{2}$.
故选C.
点评 此题主要考查了三角形面积的运算,作出恰当的辅助线得到三角形的底和高是解答此题的关键.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案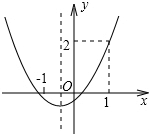 已知抛物线y=ax2+bx+c的图象如图所示,则下列结论中正确是( )
已知抛物线y=ax2+bx+c的图象如图所示,则下列结论中正确是( )| A. | a+b+c>2 | B. | 2a-b<0 | C. | b<1 | D. | 3a+c>2 |
| A. | x3•x2=x6 | B. | (x2)3=x6 | C. | x2+x3=x5 | D. | (2x2)3=6x6 |
| A. | 5x-3x=2 | B. | x4•x=x5 | C. | (-a2)4=a6 | D. | 2x3÷$\frac{1}{2}$x=4x4 |
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
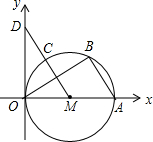 如图,直径为OA的圆M与x轴交于点O,A,点B,C把半圆OA分为三等份,连接MC并延长交y轴于点D.
如图,直径为OA的圆M与x轴交于点O,A,点B,C把半圆OA分为三等份,连接MC并延长交y轴于点D. 将如图所示的Rt△ABC绕直角边AB旋转一周,则所得几何体的主视图为( )
将如图所示的Rt△ABC绕直角边AB旋转一周,则所得几何体的主视图为( )



 如图,已知抛物线y=x2+bx+c经过A(0,-1)、B(4,-3)两点.
如图,已知抛物线y=x2+bx+c经过A(0,-1)、B(4,-3)两点.