题目内容
1.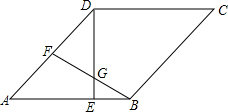 如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,DE、BF相交于点G,连接CG.
如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,DE、BF相交于点G,连接CG.(1)求∠CBG的度数;
(2)求证:BG+DG=CG.
分析 (1)连接BD,由菱形的性质得出AB=AD,AD∥BC,AB∥CD,∠BCD=∠A=60°,再证明△ABD是等边三角形,由等边三角形的三线合一性质得出BF⊥AD,得出BF⊥BC即可;
(2)由HL证明Rt△CDG≌Rt△CBG,得出对应角相等∠DCG=∠BCG=$\frac{1}{2}$∠BCD=30°,再由含30°角的直角三角形的性质即可得出结论.
解答 (1)解:连接BD,如图所示: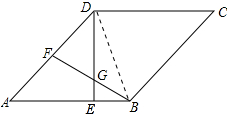 ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴AB=AD,AD∥BC,AB∥CD,∠BCD=∠A=60°,
∵∠A=60°,
∴△ABD是等边三角形,
∵F是AD的中点,
∴BF⊥AD,
∴BF⊥BC,
∴∠CBG=90°;
(2)证明:∵△ABD是等边三角形,E、F分别是AB、AD的中点,
∴DE⊥AB,BF⊥AD,
∴DE⊥CD,BF⊥BC,
∴∠CDG=∠CBG=90°,
在Rt△CDG和Rt△CBG中,$\left\{\begin{array}{l}{CG=CG}&{\;}\\{CD=CB}&{\;}\end{array}\right.$,
∴Rt△CDG≌Rt△CBG(HL),
∴∠DCG=∠BCG=$\frac{1}{2}$∠BCD=30°,BG=DG,
∴BG=$\frac{1}{2}$CG,DG=$\frac{1}{2}$CG,
∴BG+DG=CG.
点评 本题考查了菱形的性质、全等三角形的判定与性质、等边三角形的判定与性质;熟练掌握菱形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
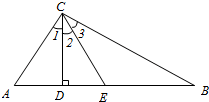 已知,如图,△ABC中,CD,CE分别是AB边上的高和中线,且∠1=∠2=∠3,求△ABC各内角的度数.
已知,如图,△ABC中,CD,CE分别是AB边上的高和中线,且∠1=∠2=∠3,求△ABC各内角的度数.
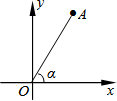 如图,点A(3,t)在第一象限,OA与x轴所夹的锐角为α,tanα=$\frac{3}{2}$,则t的值是$\frac{9}{2}$.
如图,点A(3,t)在第一象限,OA与x轴所夹的锐角为α,tanα=$\frac{3}{2}$,则t的值是$\frac{9}{2}$.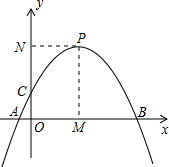 如图,开口向下的抛物线y=a(x-2)2+k,交x轴于点A、B(点A在点B左侧),交y轴正半轴于点C,顶点为P,过顶点P,作x轴,y轴的垂线,垂足分别为M,N.
如图,开口向下的抛物线y=a(x-2)2+k,交x轴于点A、B(点A在点B左侧),交y轴正半轴于点C,顶点为P,过顶点P,作x轴,y轴的垂线,垂足分别为M,N.