题目内容
11.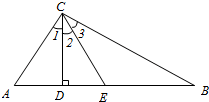 已知,如图,△ABC中,CD,CE分别是AB边上的高和中线,且∠1=∠2=∠3,求△ABC各内角的度数.
已知,如图,△ABC中,CD,CE分别是AB边上的高和中线,且∠1=∠2=∠3,求△ABC各内角的度数.
分析 首先根据∠1=∠2,且CD⊥AB,判断出AC=CE,AD=DE,∠CEA=∠A;然后根据全等三角形的判定方法,判断出△CDE≌△CFE,推得∠CED=∠CEF,DE=EF=AD;最后在Rt△BEF中,求出∠B、∠BEF,进而求出∠A的度数是多少;再根据内角和定理,求出∠ACB的度数即可.
解答 解:如图,过E作EF⊥BC于F,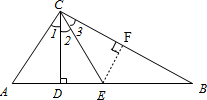 ,
,
∵∠1=∠2,且CD⊥AB,
∴AC=CE,AD=DE,∠CEA=∠A,
在△CDE和△CFE中,
$\left\{\begin{array}{l}{∠2=∠3}\\{∠CDE=∠CFE}\\{CE=CE}\end{array}\right.$,
∴△CDE≌△CFE,
∴∠CED=∠CEF,DE=EF=AD=$\frac{AE}{2}$=$\frac{BE}{2}$,
∵在Rt△BEF中,EF=$\frac{BE}{2}$,
∴∠B=30°,∠BEF=90°-30°=60°,
∴∠A=∠CED=∠CEF=(180°-∠BEF)÷2=(180°-60°)÷2=60°,
∴∠ACB=180°-∠A-∠B=180°-60°-30°=90°,
∴∠A=60°,∠ACB=90°,∠B=30°.
点评 (1)此题主要考查了三角形的内角和定理,要熟练掌握,解答此题的关键是要明确:三角形内角和是180°.
(2)此题还考查了全等三角形的判定和性质的应用,以及直角三角形的性质和应用,要熟练掌握.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
19.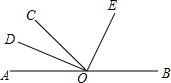 ∠AOC与∠BOC是邻补角,OD、OE分别是∠AOC与∠BOC的平分线,试判断OD与OE的夹角为( )度.
∠AOC与∠BOC是邻补角,OD、OE分别是∠AOC与∠BOC的平分线,试判断OD与OE的夹角为( )度.
 ∠AOC与∠BOC是邻补角,OD、OE分别是∠AOC与∠BOC的平分线,试判断OD与OE的夹角为( )度.
∠AOC与∠BOC是邻补角,OD、OE分别是∠AOC与∠BOC的平分线,试判断OD与OE的夹角为( )度.| A. | 60° | B. | 65° | C. | 90° | D. | 80° |
6.给定下列图形可以确定一个圆的是( )
| A. | 已知圆心 | B. | 已知半径 | C. | 已知直径 | D. | 三个点 |
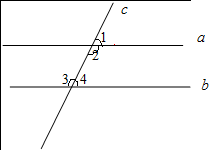 如图,因为a∥b,所以∠1=∠4,理由是两直线平行,同位角相等.
如图,因为a∥b,所以∠1=∠4,理由是两直线平行,同位角相等.
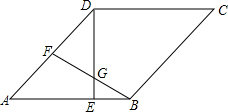 如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,DE、BF相交于点G,连接CG.
如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,DE、BF相交于点G,连接CG.