题目内容
13．若|a+b-6|+（ab-4）2=0，求-a3b-2a2b2-ab3的值．分析 根据非负数的性质得到a+b=6，ab=4．然后整体代入整理后的代数式进行求值．整理后的代数式为：-a3b-2a2b2-ab3=-ab（a+b）2．
解答 解：∵|a+b-6|+（ab-4）2=0，
∴a+b-6=0且ab-4=0，
则a+b=6，ab=4．
∴-a3b-2a2b2-ab3
=-ab（a2+2ab+b2）
=-ab（a+b）2
=-4×62
=-144．
即：-a3b-2a2b2-ab3=-144．
点评 本题考查了因式分解的应用．根据非负数的性质得到a+b=6，ab=4是解题的突破口．
练习册系列答案
相关题目
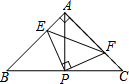如图，在Rt△ABC中，∠BAC=90°，AB=AC，直角∠EPF的顶点P是BC的中点，将∠EPF绕顶点P旋转，两边PE，PF分别交AB，AC于点E，F．下列四个结论：
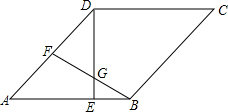如图，在菱形ABCD中，∠A=60°，E、F分别是AB、AD的中点，DE、BF相交于点G，连接CG．
“奔跑吧，兄弟！”节目组，预设计一个新的游戏：“奔跑”路线需经A、B、C、D四地．如图，其中A、B、C三地在同一直线上，D地在A地北偏东30°方向、在C地北偏西45°方向．C地在A地北偏东75°方向．且BC=CD=20m．