题目内容
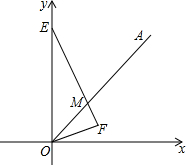 如图,OA为第一象限的角平分线,点E在y轴上,∠OEF=∠AOF,FE⊥OF交OA于M点.求证:EM=2OF.
如图,OA为第一象限的角平分线,点E在y轴上,∠OEF=∠AOF,FE⊥OF交OA于M点.求证:EM=2OF.考点:全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:作EP⊥OA,延长EP,OF,交于点Q,由OA为第一象限角平分线,得到∠AOE=45°,即三角形EPO为等腰直角三角形,即EP=OP,利用两对角相等的两三角形相似得到三角形OMF与三角形PME相似,得到∠PEM=∠POQ,再由一对直角相等,EP=OP,得到三角形EPM与三角形POQ全等,得到EM=OQ,由已知角相等,等量代换得到∠OEF=∠PEM,再由一对直角相等,夹边EF为公共边,利用ASA得到三角形EFO与三角形EFQ全等,得到OF=FQ,即OQ=2OF,等量代换即可得证.
解答: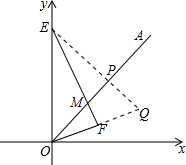 证明:作EP⊥OA,延长EP,OF,交于点Q,
证明:作EP⊥OA,延长EP,OF,交于点Q,
∵OA为第一象限得角平分线,
∴∠AOE=45°,
∴△OPE为等腰直角三角形,
∴EP=OP,
∵EF⊥OF,
∴∠EFO=∠EPM=90°,
∵∠OMF=∠EMP,
∴∠POQ=∠PEM,
∵∠OEF=∠POQ,
∴∠OEF=∠PEM,
在△OEF和△QEF中,
,
∴△OEF≌△QEF(ASA),
∴OF=FQ,即OQ=2OF,
在△POQ和△PEM中,
,
∴△POQ≌△PEM(ASA),
∴EM=OQ,
则EM=2OF.
 证明:作EP⊥OA,延长EP,OF,交于点Q,
证明:作EP⊥OA,延长EP,OF,交于点Q,∵OA为第一象限得角平分线,
∴∠AOE=45°,
∴△OPE为等腰直角三角形,
∴EP=OP,
∵EF⊥OF,
∴∠EFO=∠EPM=90°,
∵∠OMF=∠EMP,
∴∠POQ=∠PEM,
∵∠OEF=∠POQ,
∴∠OEF=∠PEM,
在△OEF和△QEF中,
|
∴△OEF≌△QEF(ASA),
∴OF=FQ,即OQ=2OF,
在△POQ和△PEM中,
|
∴△POQ≌△PEM(ASA),
∴EM=OQ,
则EM=2OF.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
 如图,与∠1成内错角的角有( )
如图,与∠1成内错角的角有( )| A、2个 | B、3个 | C、4个 | D、5个 |
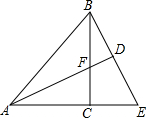 如图,BC为△ABE的高,F在BC上,且AC=BC,CE=CF,延长AF交BE于D,若AB=AE,且BE=8cm.求△AFB的面积.
如图,BC为△ABE的高,F在BC上,且AC=BC,CE=CF,延长AF交BE于D,若AB=AE,且BE=8cm.求△AFB的面积.
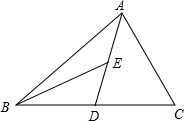 如图,AD为△ABC的中线,BE为△ABD的角平分线.
如图,AD为△ABC的中线,BE为△ABD的角平分线. 如图,已知弦AB、CD相交于P点,且∠AOC=44°,∠BOD=46°.则∠APC的度数是
如图,已知弦AB、CD相交于P点,且∠AOC=44°,∠BOD=46°.则∠APC的度数是