题目内容
抛物线的形状和开口方向与y=3x2相同,顶点是(2,3),该抛物线解析式为 .
考点:待定系数法求二次函数解析式
专题:计算题
分析:根据抛物线与已知抛物线形状开口相同,确定出a=3,再由顶点坐标,写出顶点形式即可.
解答:解:根据题意得:抛物线解析式为y=3(x-2)2+3=3x2-12x+15.
故答案为:y=3x2-12x+15
故答案为:y=3x2-12x+15
点评:此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
实数
,π,
,
,-
中,有理数有( )
| 2 |
| 5 |
| 9 |
| 13 |
| 3 | 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
当-1<x<0时,x2、x、
之间的大小关系是( )
| 1 |
| x |
A、
| ||
B、x2<x<
| ||
C、
| ||
D、x<x2<
|
下列各式中,是最简二次根式的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
为了应用乘法公式计算(x-2y+1)(x+2y-1),下列变形中正确的是( )
| A、[x-(2y+1)]2 |
| B、[x-(2y-1)][x+(2y-1)] |
| C、[(x-2y)+1][(x-2y)-1] |
| D、[x+(2y-1)]2 |
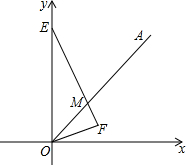 如图,OA为第一象限的角平分线,点E在y轴上,∠OEF=∠AOF,FE⊥OF交OA于M点.求证:EM=2OF.
如图,OA为第一象限的角平分线,点E在y轴上,∠OEF=∠AOF,FE⊥OF交OA于M点.求证:EM=2OF.