题目内容
设三个互不相等的有理数,既可分别表示为1,a+b,a的形式,又可分别表示为0,
,b的形式,则a2004+b2001= .
| a |
| b |
考点:有理数
专题:
分析:根据题意,可得方程组,根据解方程组,可得a、b的值,再根据乘方运算,可得幂.
解答:解:∵三个互不相等的有理数,
∴a≠0(a=0时,
=0,与三个数互不相等矛盾),
∵1≠0
∴a+b=0,
∴a=-b,
=1,
∴
,
解得
,
a2004+b2001=(-1)2014+12001=1+1=2,
故答案为:2.
∴a≠0(a=0时,
| a |
| b |
∵1≠0
∴a+b=0,
∴a=-b,
| a |
| b |
∴
|
解得
|
a2004+b2001=(-1)2014+12001=1+1=2,
故答案为:2.
点评:本题考查了有理数,根据题意得出方程组是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 某反比例函数的图象如图所示,求此反比例函数的解析式,并写出点A关于原点对称的坐标.
某反比例函数的图象如图所示,求此反比例函数的解析式,并写出点A关于原点对称的坐标. 如图(1),BP、CP分别是△ABC的内、外角平分线.
如图(1),BP、CP分别是△ABC的内、外角平分线. 在正方形ABCD中,M是AD的中点,∠NMB=∠CBM,则CN:DN=
在正方形ABCD中,M是AD的中点,∠NMB=∠CBM,则CN:DN= 某工厂生产一种产品,当生产数量至少为10吨,但不超过50吨时,每吨的成本y(万元/吨)与生产数量x(吨)的函数关系的图象如图所示.
某工厂生产一种产品,当生产数量至少为10吨,但不超过50吨时,每吨的成本y(万元/吨)与生产数量x(吨)的函数关系的图象如图所示. 如图,△ABC中,BE平分∠ABC,DE∥BC交于AB于点D,BC=6,AB=9,求DE的长.
如图,△ABC中,BE平分∠ABC,DE∥BC交于AB于点D,BC=6,AB=9,求DE的长.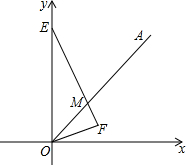 如图,OA为第一象限的角平分线,点E在y轴上,∠OEF=∠AOF,FE⊥OF交OA于M点.求证:EM=2OF.
如图,OA为第一象限的角平分线,点E在y轴上,∠OEF=∠AOF,FE⊥OF交OA于M点.求证:EM=2OF.