题目内容
18．
如图，D为AB的中点，E为AC上一点，DE的延长线交BC的延长线于F，求证：$\frac{BF}{CF}$=$\frac{AE}{EC}$．
分析 作CG∥AB交DF于G，由中点的定义得出AD=BD，由平行线得出BDF∽△CGF，△ADE∽△CGE，得出对应边成比例$\frac{BF}{CF}=\frac{BD}{CG}$，$\frac{AE}{EC}=\frac{AD}{CG}$，即可得出结论．
解答 证明：作CG∥AB交DF于G，如图所示：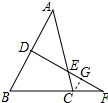
∵D为AB的中点，
∴AD=BD，
∵CG∥AB，
∴BDF∽△CGF，△ADE∽△CGE，
∴$\frac{BF}{CF}=\frac{BD}{CG}$，$\frac{AE}{EC}=\frac{AD}{CG}$，
∴$\frac{BF}{CF}$=$\frac{AE}{EC}$．
点评 本题考查了相似三角形的判定与性质；通过作辅助线证明三角形相似是解决问题的关键．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目