题目内容
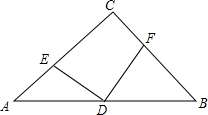
5. 已知:在?ABCD中,E、F分别为AD、BC边的中点,连接BE、DF交AC于G、H点.求证:GC=2AG.
已知:在?ABCD中,E、F分别为AD、BC边的中点,连接BE、DF交AC于G、H点.求证:GC=2AG.
分析 根据平行四边形的性质得到AD=BC,AD∥BC,由E、F分别为AD、BC边的中点,得到DE=$\frac{1}{2}$AD,BF=$\frac{1}{2}$BC,推出四边形BFDE是平行四边形,根据平行四边形的性质得到BE∥DF,然后根据平行线分线段成比例即可得到结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵E、F分别为AD、BC边的中点,
∴DE=$\frac{1}{2}$AD,BF=$\frac{1}{2}$BC,
∴DE∥BF,DE=BF,
∴四边形BFDE是平行四边形,
∴BE∥DF,
∴AG=GH,CH=GH,
∴GC=2AG.
点评 本题考查了平行四边形的性质和判定,平行线分线段成比例定理,熟练掌握平行线分线段成比例定理是解题的关键.

练习册系列答案
相关题目
20.下列两个变量之间不存在函数关系的是( )
| A. | 圆的面积S和半径R之间的关系 | |
| B. | 匀速行驶的汽车,行驶的路程s与时间t之间的关系 | |
| C. | 一个正数的平方根与它本身之间的关系 | |
| D. | 电阻一定,加在这个电阻两端的电压通过这个电阻的电流之间的关系 |
 实数a、b在数轴上的位置如图所示,请化简:|a-b|-2$\sqrt{{a}^{2}}$+$\sqrt{{b}^{2}}$.
实数a、b在数轴上的位置如图所示,请化简:|a-b|-2$\sqrt{{a}^{2}}$+$\sqrt{{b}^{2}}$.
 如图,△ABC中,∠C=90°,CA=CB,D是AB的中点,AE=CF.
如图,△ABC中,∠C=90°,CA=CB,D是AB的中点,AE=CF.