Question

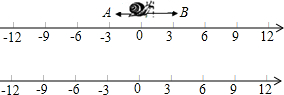
13．实数a、b在数轴上的位置如图所示，请化简：|a-b|-2$\sqrt{{a}^{2}}$+$\sqrt{{b}^{2}}$．

Answer 1

分析 先根据数轴可知a＜0＜b，进而可求a-b＜0，再根据绝对值的概念、二次根式的性质进行计算．

解答 解：根据数轴可知a＜0＜b，
所以a-b＜0，
则：|a-b|-2$\sqrt{{a}^{2}}$+$\sqrt{{b}^{2}}$=-（a-b）+2a+b=-a+b+2a+b=a+2b．

点评 此题主要考查了实数与数轴，绝对值的概念，二次根式的性质与化简，正确化简二次根式是解题关键．