题目内容
17.在桌上摆着一个由若干个相同的小正方体组合在一起的一个几何体,其从左面和上面分别看到如图所示的不同的图形.(1)组成这个几何体的小立方体块数最多需要12块,最少需要10块.
(2)若每个小正方体的棱长都为2cm,则组成这个几何体块数最多时的表面积是160cm2.(包含底面)
(3)请画出从正面看这个几何体所得到的所有可能的平面图形.
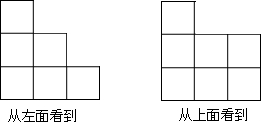
分析 (1)根据从上面看到的图形可知,这个几何体有3行3列,底层有7个小正方体;根据从左面看到的图形可知,这个几何体有三层,第三层有1个小正方体,第二层最少有2个小正方体,最多有4个小正方体,据此即可解答;
(2)从上面和下面看,各有7个正方形面;从左面和右面看,各有6个正方形面;组成这个几何体块数最多时,从前面和后面看,各有7个正方形面,一共有40个正方形面,一个正方形面的面积是2×2=4平方厘米,据此即可求出这个几何体的表面积;
(3)根据(1)即可画出从正面看到的图形的所有可能.
解答 解:(1)综合俯视图和左视图,这个几何体的底层有7个小正方体,第二层最少有2个小正方体,最多有4个小正方体,第三层有1个小正方体,
所以组成这个几何体的小正方块最多有7+4+1=12块,最少有7+2+1=10块;
(2)若每个小正方体的棱长都为2cm,则组成这个几何体块数最多时的表面积是
(2×2)×(7×2+6×2+7×2)=4×40=160(平方厘米);
(3)主视图可能有以下情况:



故答案为:12,10;160.
点评 此题考查了三视图和表面积,从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力.

练习册系列答案
相关题目
8.已知下列结论:
①将直角三角形的三边同时扩大2倍,得到的一个钝角三角形;
②在平面直角坐标系中点A(2,3)与点B(3,2)表示不同的点;
③实数与数轴上的点一一对应;
④有理数有无限个,无理数有有限个.
其中正确的结论是( )
①将直角三角形的三边同时扩大2倍,得到的一个钝角三角形;
②在平面直角坐标系中点A(2,3)与点B(3,2)表示不同的点;
③实数与数轴上的点一一对应;
④有理数有无限个,无理数有有限个.
其中正确的结论是( )
| A. | ①② | B. | ②③ | C. | ③④ | D. | ②③④ |
12. 如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=( )
如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=( )
 如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=( )
如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
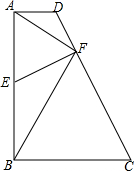 如图,已知四边形ABCD中,AB⊥BC,AD∥BC,E为AB的中点,EF⊥CD于F,且EF=$\frac{1}{2}$AB,连接AF,BF,在不添加辅助线和字母情况下,按要求完成下列各题
如图,已知四边形ABCD中,AB⊥BC,AD∥BC,E为AB的中点,EF⊥CD于F,且EF=$\frac{1}{2}$AB,连接AF,BF,在不添加辅助线和字母情况下,按要求完成下列各题 已知:在?ABCD中,E、F分别为AD、BC边的中点,连接BE、DF交AC于G、H点.求证:GC=2AG.
已知:在?ABCD中,E、F分别为AD、BC边的中点,连接BE、DF交AC于G、H点.求证:GC=2AG.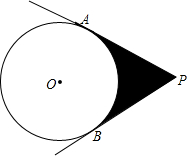 如图,PA、PB为⊙O的切线,⊙O的半径为2,∠P=60°.阴影部分的周长是$\frac{4}{3}$π+4$\sqrt{3}$,面积是4$\sqrt{3}$-$\frac{4}{3}$π.
如图,PA、PB为⊙O的切线,⊙O的半径为2,∠P=60°.阴影部分的周长是$\frac{4}{3}$π+4$\sqrt{3}$,面积是4$\sqrt{3}$-$\frac{4}{3}$π. 如图,在四边形ABCD中,AB=2,CD=1,∠A=60°,求AD的长与四边形ABCD的面积.
如图,在四边形ABCD中,AB=2,CD=1,∠A=60°,求AD的长与四边形ABCD的面积.