题目内容
14.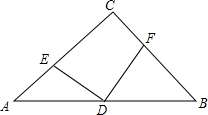 如图,△ABC中,∠C=90°,CA=CB,D是AB的中点,AE=CF.
如图,△ABC中,∠C=90°,CA=CB,D是AB的中点,AE=CF.(1)猜想:DE与DF的数量和位置关系分别为相等、垂直;
(2)证明你的猜想.
分析 (1)根据图形可得猜想DE=DF,DE⊥DF;
(2)首先根据等腰三角形三线合一的性质可得∠DCF=$\frac{1}{2}∠$ACB=45°,由直角三角形的性质可得AD=CD,然后证明△AED≌△CFD可得ED=DF,∠EDA=∠CDF,再证明△DFB≌△DEC可得∠EDC=∠FDB,进而可得到ED⊥DF.
解答  (1)解:DE=DF,DE⊥DF;
(1)解:DE=DF,DE⊥DF;
(2)证明:连接CD,
∵CA=CB,∠C=90°,
∴∠A=45°,
∵D是AB的中点,∠C=90°,
∴AD=CD,
∵CA=CB,D是AB的中点,
∴∠DCF=$\frac{1}{2}∠$ACB=45°,
在△AED和△CFD中$\left\{\begin{array}{l}{CD=AD}\\{∠A=∠DCF}\\{AE=CF}\end{array}\right.$,
∴△AED≌△CFD(SAS),
∴ED=DF,
∴∠EDA=∠CDF,∠AED=∠DFC,
∴∠CED=∠DFB,
∵AC=BC,AE=CF,
∴CE=BF,
在△CED和△BFD中$\left\{\begin{array}{l}{CE=BF}\\{∠CED=∠BFD}\\{ED=DF}\end{array}\right.$,
∴△DFB≌△DEC(SAS),
∴∠EDC=∠FDB,
∵∠ADE+∠EDC+∠CDF+∠FDB=180°,
∴∠EDF=90°,
∴ED⊥DF.
点评 本题主要考查等腰三角形的性质、直角三角形的性质,以及全等三角形的判定和性质,关键是熟练掌握全等三角形的判定方法:SSS、SAS、ASA、AAS、HL.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
4.在长为3,4,5,12,13的线段中任意取三条可构成( ) 个直角三角形.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
 已知:在?ABCD中,E、F分别为AD、BC边的中点,连接BE、DF交AC于G、H点.求证:GC=2AG.
已知:在?ABCD中,E、F分别为AD、BC边的中点,连接BE、DF交AC于G、H点.求证:GC=2AG.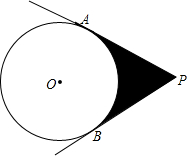 如图,PA、PB为⊙O的切线,⊙O的半径为2,∠P=60°.阴影部分的周长是$\frac{4}{3}$π+4$\sqrt{3}$,面积是4$\sqrt{3}$-$\frac{4}{3}$π.
如图,PA、PB为⊙O的切线,⊙O的半径为2,∠P=60°.阴影部分的周长是$\frac{4}{3}$π+4$\sqrt{3}$,面积是4$\sqrt{3}$-$\frac{4}{3}$π.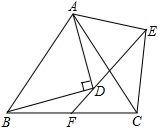 △ABC与△ADE都是以点A为顶点的等腰三角形,且∠BAC=∠DAE,BD⊥AD,ED的延长线交BC于点F,
△ABC与△ADE都是以点A为顶点的等腰三角形,且∠BAC=∠DAE,BD⊥AD,ED的延长线交BC于点F, 如图,在四边形ABCD中,AB=2,CD=1,∠A=60°,求AD的长与四边形ABCD的面积.
如图,在四边形ABCD中,AB=2,CD=1,∠A=60°,求AD的长与四边形ABCD的面积.
 有3个正整数解,则
有3个正整数解,则 的取值范围是:( )
的取值范围是:( ) 6 B.
6 B.  C.
C.  D.
D. 