题目内容
16.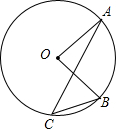 如图,⊙O上A、B、C三点,若∠B=50°,∠A=20°,则∠AOB等于( )
如图,⊙O上A、B、C三点,若∠B=50°,∠A=20°,则∠AOB等于( )| A. | 30° | B. | 50° | C. | 60° | D. | 70° |
分析 设∠C=x,根据圆周角定理得出∠AOB=2∠C=2x.由对顶角相等得到∠1=∠2,根据三角形内角和定理得出∠A+∠AOB=∠B+∠C,依此列出关于x的方程,求解即可.
解答 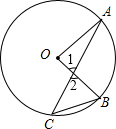 解:设∠C=x,则∠AOB=2∠C=2x.
解:设∠C=x,则∠AOB=2∠C=2x.
∵∠1=∠2,
∴∠A+∠AOB=∠B+∠C,
即20°+2x=50°+x,
解得x=30°,
∴∠AOB=2x=60°.
故选C.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了三角形内角和定理,设∠C=x,根据三角形内角和定理列出关于x的方程是解题的关键.

练习册系列答案
相关题目
7.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4.如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的三倍,则称这样的方程为“3倍根方程”,以下说法不正确的是( )
| A. | 方程x2-4x+3=0是3倍根方程 | |
| B. | 若关于x的方程(x-3)(mx+n)=0是3倍根方程,则m+n=0 | |
| C. | 若m+n=0且m≠0,则关于x的方程(x-3)(mx+n)=0是3倍根方程 | |
| D. | 若3m+n=0且m≠0,则关于x的方程x2+(m-n)x-mn=0是3倍根方程 |
17. 如图,二次函数y=ax2+bx+c(a≠0)的大致图象,关于该二次函数下列说法正确的是( )
如图,二次函数y=ax2+bx+c(a≠0)的大致图象,关于该二次函数下列说法正确的是( )
 如图,二次函数y=ax2+bx+c(a≠0)的大致图象,关于该二次函数下列说法正确的是( )
如图,二次函数y=ax2+bx+c(a≠0)的大致图象,关于该二次函数下列说法正确的是( )| A. | a>0,b<0,c>0 | B. | 当-1<x<2时,y>0 | ||
| C. | b2-4ac<0 | D. | 当x<$\frac{1}{2}$时,y随x的增大而减小 |
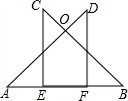 如图,A,E,F,B在同一条直线上,CE⊥AB,DF⊥AB,AE=BF,∠A=∠B,求证:OC=OD.
如图,A,E,F,B在同一条直线上,CE⊥AB,DF⊥AB,AE=BF,∠A=∠B,求证:OC=OD.