题目内容
20.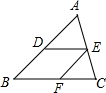 如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是( )
如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是( )| A. | $\frac{AD}{BD}$=$\frac{DE}{BC}$ | B. | $\frac{BF}{BC}$=$\frac{EF}{AD}$ | C. | $\frac{AE}{EC}$=$\frac{BF}{CF}$ | D. | $\frac{EF}{AB}$=$\frac{DE}{BC}$ |
分析 根据平行线分线段成比例定理找准线段的对应关系,对各选项分析判断后利用排除法求解.
解答 解:∵DE∥BC,
∴$\frac{DE}{BC}=\frac{AD}{AB}$,BD≠BC,
∴$\frac{AD}{BD}≠\frac{DE}{BC}$,选项A不正确;
∵DE∥BC,EF∥AB,
∴$\frac{BF}{BC}=\frac{AE}{AC}$,EF=BD,$\frac{EF}{AD}=\frac{BD}{AD}$,
∵$\frac{AE}{AC}$≠$\frac{BD}{AD}$,
∴$\frac{BF}{BC}≠\frac{EF}{AD}$,选项B不正确;
∵EF∥AB,
∴$\frac{AE}{EC}=\frac{BF}{CF}$,选项C正确;
∵DE∥BC,EF∥AB,
∴$\frac{EF}{AB}=\frac{CE}{AC}$,$\frac{DE}{BC}$=$\frac{AE}{AC}$,CE≠AE,
∴$\frac{EF}{AB}≠\frac{DE}{BC}$,选项D不正确;
故选:C.
点评 本题考查了平行线分线段成比例定理;熟练掌握平行线分线段成比例定理,在解答时寻找对应线段是关健.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.不等式组$\left\{\begin{array}{l}{3(x-1)<-6}\\{\frac{3-x}{2}≤1}\end{array}\right.$的解集是( )
| A. | x≥1 | B. | -1<x<1 | C. | x<-1 | D. | 无解 |
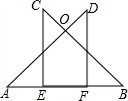 如图,A,E,F,B在同一条直线上,CE⊥AB,DF⊥AB,AE=BF,∠A=∠B,求证:OC=OD.
如图,A,E,F,B在同一条直线上,CE⊥AB,DF⊥AB,AE=BF,∠A=∠B,求证:OC=OD.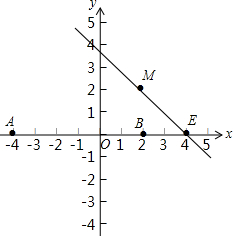 如图,x轴上两个点A(-4,0),B(2,0),直线l经过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.
如图,x轴上两个点A(-4,0),B(2,0),直线l经过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.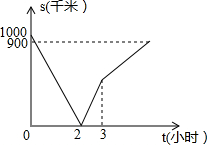 甲、乙、丙三地在一条直线上,乙地在甲地和丙地之间,一列高速列车从甲地开往乙地,一列快速列车从丙地经乙地开往甲地,两列列车同时出发,匀速行驶,且到达各自目的地后停止运行,从两列列车出发开始,至快速列车到达甲地为止,两列列车的距离s(千米)与行驶时间t(小时)之间的函数图象如图所示
甲、乙、丙三地在一条直线上,乙地在甲地和丙地之间,一列高速列车从甲地开往乙地,一列快速列车从丙地经乙地开往甲地,两列列车同时出发,匀速行驶,且到达各自目的地后停止运行,从两列列车出发开始,至快速列车到达甲地为止,两列列车的距离s(千米)与行驶时间t(小时)之间的函数图象如图所示