题目内容
17．己知x+y=-3，求代数式$\frac{xy+y{\;}^{2}}{x-y}$÷$\frac{y}{{x}^{2}-{y}^{2}}$的值．分析 先根据分式混合运算的法则把原式进行化简，再把x+y=-3代入进行计算即可．
解答 解：原式=$\frac{y（x+y）}{x-y}$•$\frac{（x+y）（x-y）}{y}$
=（x+y）2，
当x+y=-3时，原式=9．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
相关题目
7．下列四个图形中，既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
12．不等式组$\left\{\begin{array}{l}{3（x-1）＜-6}\\{\frac{3-x}{2}≤1}\end{array}\right.$的解集是（ ）
| A． | x≥1 | B． | -1＜x＜1 | C． | x＜-1 | D． | 无解 |
2．皖星书店年初以每本20元的价格购进一批畅销书《莫言精品集》，销售过程中发现，每月销售量y（本）与销售单价x（元）之间的关系如表所示，按照表中y与x的关系规律，解决下面的问题：
（1）试求出y与x的函数关系式．
（2）销售单价在什么范围时，书店能盈利？
（3）如果想要每月获得的利润不低于2000元，那么该书店每月的成本最少需要多少元？（成本=每本进价×销售量）
| x | 25 | 28 | 30 | 32 | 35 |
| y | 250 | 220 | 200 | 180 | 150 |
（2）销售单价在什么范围时，书店能盈利？
（3）如果想要每月获得的利润不低于2000元，那么该书店每月的成本最少需要多少元？（成本=每本进价×销售量）
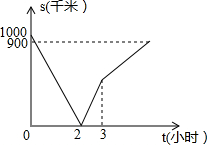甲、乙、丙三地在一条直线上，乙地在甲地和丙地之间，一列高速列车从甲地开往乙地，一列快速列车从丙地经乙地开往甲地，两列列车同时出发，匀速行驶，且到达各自目的地后停止运行，从两列列车出发开始，至快速列车到达甲地为止，两列列车的距离s（千米）与行驶时间t（小时）之间的函数图象如图所示
17．
如图，二次函数y=ax2+bx+c（a≠0）的大致图象，关于该二次函数下列说法正确的是（ ）
如图，二次函数y=ax2+bx+c（a≠0）的大致图象，关于该二次函数下列说法正确的是（ ）| A． | a＞0，b＜0，c＞0 | B． | 当-1＜x＜2时，y＞0 | ||
| C． | b2-4ac＜0 | D． | 当x＜$\frac{1}{2}$时，y随x的增大而减小 |
我们新定义一种三角形：两边平方和等于第三边平方的4倍的三角形叫做常态三角形．例如：某三角形三边长分别是5，6和8，因为62+82=4×52=100，所以这个三角形是常态三角形．