题目内容
 如图所示,DE∥BC,AC=12,AD=
如图所示,DE∥BC,AC=12,AD=| 2 |
| 3 |
考点:平行线分线段成比例
专题:计算题
分析:先利用平行线分线段成比例,由DE∥BC得
=
,根据比例性质可计算出AE,然后利用EC=AC-AE求解.
| AD |
| AB |
| AE |
| AC |
解答:解:∵DE∥BC,
∴
=
,即
=
,
∴AE=8,
∴EC=AC-AE=12-8=4.
故答案为4.
∴
| AD |
| AB |
| AE |
| AC |
| AE |
| 12 |
| 2 |
| 3 |
∴AE=8,
∴EC=AC-AE=12-8=4.
故答案为4.
点评:本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.

练习册系列答案
相关题目
已知点A(4,3)和点B是坐标平面内的两个点,且它们关于过点(-3,0)与y轴平行的直线对称,则点B的坐标是( )
| A、(1,3) |
| B、(-10,3) |
| C、(4,3) |
| D、(4,1) |
 如图,在△ABC中,M为AC中点,连接BM,点D为BM上的一点,过点C作CE∥BM,过点D作DE∥AB,CE、DE交于点E,连接BE,求证:BE=AD.
如图,在△ABC中,M为AC中点,连接BM,点D为BM上的一点,过点C作CE∥BM,过点D作DE∥AB,CE、DE交于点E,连接BE,求证:BE=AD.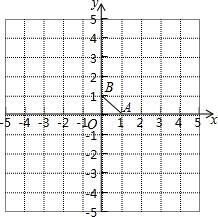 如果将点P绕定点M旋转180°后与点Q重合,那么称点P与点Q关于M对称,定点M叫做对称中心.此时,点M是线段PQ的中点.在平面直角坐标系中,△ABO的顶点A,B,O的坐标分别为(1,0)、(0,1)、(0,0).点列P1、P2、P3、…,中的相邻两点都关于△ABO的一个顶点对称:点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与点P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称,…,对称中心分别是A,B,O,A,B,O,…,且这些对称中心依次循环.已知点P1的坐标是(1,1),则点P100的坐标为
如果将点P绕定点M旋转180°后与点Q重合,那么称点P与点Q关于M对称,定点M叫做对称中心.此时,点M是线段PQ的中点.在平面直角坐标系中,△ABO的顶点A,B,O的坐标分别为(1,0)、(0,1)、(0,0).点列P1、P2、P3、…,中的相邻两点都关于△ABO的一个顶点对称:点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与点P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称,…,对称中心分别是A,B,O,A,B,O,…,且这些对称中心依次循环.已知点P1的坐标是(1,1),则点P100的坐标为 如图所示,已知△ABC中,DE∥BC,AD=2,BD=5,AC=5,求AE的长.
如图所示,已知△ABC中,DE∥BC,AD=2,BD=5,AC=5,求AE的长.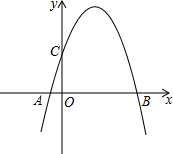 二次函数图象过A、C、B三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴正半轴上,且OB=OC.
二次函数图象过A、C、B三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴正半轴上,且OB=OC.