题目内容
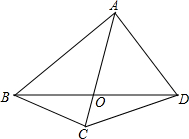如图，O是四边形ABCD对角线的交点，已知∠BAD+∠BCA=180°，AB=5，AC=4，AD=3，| BO |
| OD |
| 7 |
| 6 |
考点：相似三角形的判定与性质
专题：常规题型
分析：过D点作AO的平行线，交BA延长线于E点，构建△ADE，根据题干中条件可证明△EAD∽△ACB，可以求得BC的值．
解答：解：过D点作AO的平行线，交BA延长线于E点．
∵AO∥ED，
∴
=
，求得AE=
，
∵AO∥ED，
∴∠BAC=∠AED，
∵∠BAD+∠BCA=180°，∠BAD+∠EAD=180°，
∴∠BCA=∠EAD，
∴△EAD∽△ACB，
∴
=
，
求得BC=
．
故答案为：
．
∵AO∥ED，
∴
| BO |
| OD |
| BA |
| AE |
| 30 |
| 7 |
∵AO∥ED，
∴∠BAC=∠AED，
∵∠BAD+∠BCA=180°，∠BAD+∠EAD=180°，
∴∠BCA=∠EAD，
∴△EAD∽△ACB，
∴
| AD |
| BC |
| AE |
| AC |
求得BC=
| 7 |
| 5 |
故答案为：
| 7 |
| 5 |
点评：本题考查了相似三角形的判定，考查了相似三角形对应边比例相等的性质．
练习册系列答案
金钥匙试卷系列答案
相关题目
已知一元二次方程x2-2x-7=0的两个根为x1，x2，则x1+x2的值为（ ）
| A、-2 | B、2 | C、-7 | D、7 |
如图，7×8网格的每个小正方形边长均为1，将抛物线y1=x2-1的图象向右平移2个单位得到抛物线y2．
如图，在△ABC中，D是BC上的一点，E是AC上的一点，EF∥AD交BC于F，EG∥AB交BC于G，求证：CF•GB=CG•FD．
如图，Rt△ABC中，∠BAC=90°，AD⊥BC于D，DE⊥AB于E，求证：
如图，在△ABC中，M为AC中点，连接BM，点D为BM上的一点，过点C作CE∥BM，过点D作DE∥AB，CE、DE交于点E，连接BE，求证：BE=AD．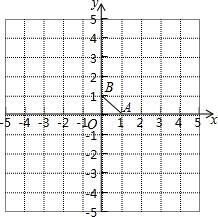
如果将点P绕定点M旋转180°后与点Q重合，那么称点P与点Q关于M对称，定点M叫做对称中心．此时，点M是线段PQ的中点．在平面直角坐标系中，△ABO的顶点A，B，O的坐标分别为（1，0）、（0，1）、（0，0）．点列P1、P2、P3、…，中的相邻两点都关于△ABO的一个顶点对称：点P1与点P2关于点A对称，点P2与点P3关于点B对称，点P3与点P4关于点O对称，点P4与点P5关于点A对称，点P5与点P6关于点B对称，点P6与点P7关于点O对称，…，对称中心分别是A，B，O，A，B，O，…，且这些对称中心依次循环．已知点P1的坐标是（1，1），则点P100的坐标为