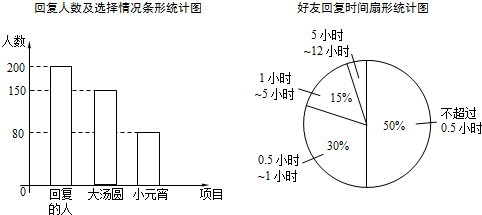
题目内容
15.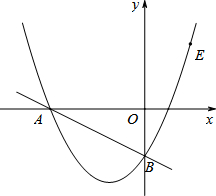 如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x-2与坐标轴分别交于A、B两点,过A、B两点的抛物线解析式为y=x2+bx+c.
如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x-2与坐标轴分别交于A、B两点,过A、B两点的抛物线解析式为y=x2+bx+c.(1)求抛物线的解析式;
(2)E为抛物线上第一象限部分上一点,当S△ABE=10时,求点E的坐标;
(3)F为直线AB下方抛物线上一点,连接AF,当∠FAB=∠BAO时,求F点坐标.
分析 (1)求出A、B坐标代入y=x2+bx+c即可解决.
(2)如图作AM∥y轴,BM∥x轴,则点M坐标为(-4,-2),根据S△AEB=S△AME+s△EBM-S△ABM=10列出方程即可解决.
(3)设点O关于直线AB的对称点G,则直线OG为y=2x,此时直线AG与抛物线交于点F,∠FAB=∠OAB,求出点G坐标后求出直线AG,解直线AB与抛物线组成的方程组即可解决问题.
解答 解:(1)直线y=-$\frac{1}{2}$x-2,令y=0,得x=-4,∴点A(-4,0),
令x=0,得y=-2,∴点B(0,-2)
把A、B两点坐标代入y=x2+bx+c得$\left\{\begin{array}{l}{16-4b+c=0}\\{c=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=\frac{7}{2}}\\{c=-2}\end{array}\right.$,
∴抛物线解析式为y=x2+$\frac{7}{2}$x-2.
(2)如图作AM∥y轴,BM∥x轴,则点M坐标为(-4,-2),连接EM,设点E(m,m2+$\frac{7}{2}$m-2),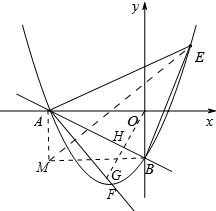 ∵S△AEB=S△AME+s△EBM-S△ABM=10,
∵S△AEB=S△AME+s△EBM-S△ABM=10,
∴$\frac{1}{2}$×2×(m+4)+$\frac{1}{2}$×4×(m2+$\frac{7}{2}$m-2+2)-$\frac{1}{2}$×2×4=10,
∴m2+4m-5=0,
∴m=1(或-5不合题意舍弃).
∴点E坐标(1,$\frac{5}{2}$).
(3)设点O关于直线AB的对称点G,则直线OG为y=2x,此时直线AG与抛物线交于点F,∠FAB=∠OAB.
由$\left\{\begin{array}{l}{y=2x}\\{y=-\frac{1}{2}x-2}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-\frac{4}{5}}\\{y=-\frac{8}{5}}\end{array}\right.$,
∴直线AB与直线OG的交点H为(-$\frac{4}{5}$,-$\frac{8}{5}$),
∴点G坐标为(-$\frac{8}{5}$,-$\frac{16}{5}$),
设直线AG为y=kx+b,则$\left\{\begin{array}{l}{-4k+b=0}\\{-\frac{8}{5}k+b=-\frac{16}{5}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=-\frac{16}{3}}\end{array}\right.$.
∴直线AG为y=-$\frac{4}{3}$x-$\frac{16}{3}$,
由$\left\{\begin{array}{l}{y=-\frac{4}{3}x-\frac{16}{3}}\\{y={x}^{2}+\frac{7}{2}x-2}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-4}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{5}{6}}\\{y=-\frac{38}{9}}\end{array}\right.$,
∴点F坐标为(-$\frac{5}{6}$,-$\frac{38}{9}$).
点评 本题考查二次函数、一次函数的有关知识、三角形的面积、对称等知识,第二个问题的关键是添加辅助线,利用S△AEB=S△AME+s△EBM-S△ABM,列出方程解决问题,学会利用解方程组求两个函数的交点坐标,求点F坐标转化为先求直线AG,本题属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案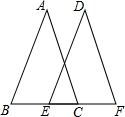 如图所示,AB=DE,AC=DF,BC=EF,小雪根据这些条件得出了四个结论,你认为叙述正确的个数是:(1)AB∥DE;(2)AC∥DF;(3)BE=CF;(4)∠DEF=∠ACB.( )
如图所示,AB=DE,AC=DF,BC=EF,小雪根据这些条件得出了四个结论,你认为叙述正确的个数是:(1)AB∥DE;(2)AC∥DF;(3)BE=CF;(4)∠DEF=∠ACB.( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
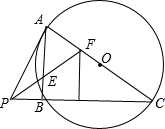 如图,已知:PA切⊙O于A,若AC为⊙O的直径,PBC为⊙O的割线,E为弦AB的中点,PE的延长线交AC于E,且∠FPB=45°,点F到PC的距离为5,则FC的长为( )
如图,已知:PA切⊙O于A,若AC为⊙O的直径,PBC为⊙O的割线,E为弦AB的中点,PE的延长线交AC于E,且∠FPB=45°,点F到PC的距离为5,则FC的长为( )| A. | 10 | B. | 12 | C. | $5\sqrt{5}$ | D. | $5\sqrt{6}$ |
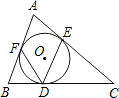 如图,△ABC的内切圆为⊙O,切点分别为D、E、F,若∠A=58°,求∠EDF的度数.
如图,△ABC的内切圆为⊙O,切点分别为D、E、F,若∠A=58°,求∠EDF的度数.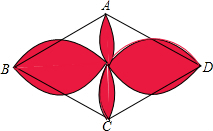 如图,四边形ABCD是菱形,AB=10cm,∠ABC=60°,分别以ABCD的四条边为直径作半圆.求图中红色部分的面积.
如图,四边形ABCD是菱形,AB=10cm,∠ABC=60°,分别以ABCD的四条边为直径作半圆.求图中红色部分的面积.