题目内容
7.在平面直角坐标系中,P点在第二象限,OP与y轴的正半轴的夹角为30°,OP=2.求P点的坐标.分析 根据题意可以画出相应的图形,根据题目中的OP的长度和∠AOP的角度,由30°角所对的直角边等于斜边的一半,可以求得AP的长,然后根据勾股定理可以求得OA的长,从而可以求得点P的坐标,本题得以解决.
解答 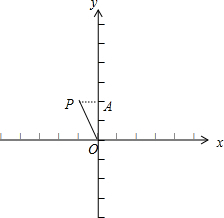 解:作PA⊥y轴于点A,如右图所示,
解:作PA⊥y轴于点A,如右图所示,
由题意可得,∠POA=30°,OP=2,
∵∠POA=90°,
∴DA=1,
∴OA=$\sqrt{O{P}^{2}-D{A}^{2}}=\sqrt{{2}^{2}-{1}^{2}}=\sqrt{3}$,
∵P点在第二象限,
∴点P的坐标为(-1,$\sqrt{3}$).
点评 本题考查勾股定理、坐标与图形的性质、含30°角的直角三角形,解题的关键是明确题意,画出相应的图形,利用数形结合的思想解答问题.

练习册系列答案
相关题目
12.下列说法正确的是( )
| A. | “明天会下雨”是必然事件 | |
| B. | 想了解“五•一”期间福州市各家庭的消费情况,适合的调查方式是抽样调查 | |
| C. | 正方形是轴对称图形,不是中心对称图形 | |
| D. | 120000用科学记数法表示是1.2×106 |
16.有四张正面分别标有数字-2,-6,2,6的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中抽取一张,将该卡片上的数字记为a;不放回,再从中抽取一张,将该卡片上的数字记为b,则使关于x的不等式组$\left\{\begin{array}{l}{\frac{3x-2}{2}<x+\frac{5}{2}}\\{ax>b}\end{array}\right.$的解集中有且只有3个非负整数解的概率( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
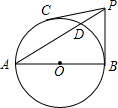 如图,AB是⊙O的直径,PB、PC是⊙O的切线,切点为B、C,连接PA交⊙O于D,∠BPC=2∠A.
如图,AB是⊙O的直径,PB、PC是⊙O的切线,切点为B、C,连接PA交⊙O于D,∠BPC=2∠A.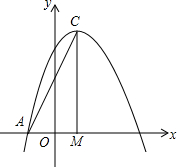 如图,已知抛物线y=-x2+bx+c与x轴的一个交点为A(-1,0),对称轴为直线x=1.
如图,已知抛物线y=-x2+bx+c与x轴的一个交点为A(-1,0),对称轴为直线x=1.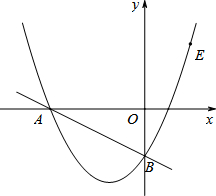 如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x-2与坐标轴分别交于A、B两点,过A、B两点的抛物线解析式为y=x2+bx+c.
如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x-2与坐标轴分别交于A、B两点,过A、B两点的抛物线解析式为y=x2+bx+c.