题目内容
5.已知:$x=\frac{{\sqrt{10}-1}}{2},y=\frac{{\sqrt{10}+1}}{2}$,则$\frac{x}{{xy-{y^2}}}-\frac{y}{{{x^2}-xy}}$的值为$\frac{{4\sqrt{10}}}{9}$.分析 先把分式通分,再把分子相加减,结果化为最减分式后把x、y的值代入进行计算即可.
解答 解:原式=$\frac{x}{y(x-y)}$-$\frac{y}{x(x-y)}$
=$\frac{{x}^{2}-{y}^{2}}{xy(x-y)}$
=$\frac{(x+y)(x-y)}{xy(x-y)}$
=$\frac{x+y}{xy}$,
当x=$\frac{\sqrt{10}-1}{2}$,y=$\frac{\sqrt{10}+1}{2}$时,原式=$\frac{\frac{\sqrt{10}-1}{2}+\frac{\sqrt{10}+1}{2}}{\frac{\sqrt{10}-1}{2}•\frac{\sqrt{10}+1}{2}}$=$\frac{\frac{2\sqrt{10}}{2}}{\frac{10-1}{4}}$=$\frac{\sqrt{10}}{\frac{9}{4}}$=$\frac{4\sqrt{10}}{9}$.
故答案为:$\frac{4\sqrt{10}}{9}$.
点评 本题考查的是分式的化简求值,此类问题一般是先化简为最简分式或整式,再代入求值.化简时不能跨度太大,而缺少必要的步骤.

练习册系列答案
相关题目
16.有四张正面分别标有数字-2,-6,2,6的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中抽取一张,将该卡片上的数字记为a;不放回,再从中抽取一张,将该卡片上的数字记为b,则使关于x的不等式组$\left\{\begin{array}{l}{\frac{3x-2}{2}<x+\frac{5}{2}}\\{ax>b}\end{array}\right.$的解集中有且只有3个非负整数解的概率( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
13.在下列6个图形中,每个小四边形都是全等的正方形,那么沿其正方形相邻边折叠,能够围成正方体的编号是( )
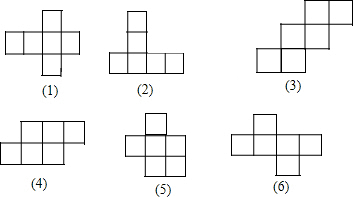

| A. | ①②③④ | B. | ①②⑥ | C. | ①③④ | D. | ①③⑥ |
15.2-1等于( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | -$\frac{1}{2}$ |
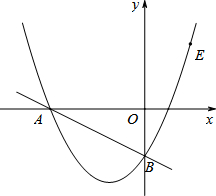 如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x-2与坐标轴分别交于A、B两点,过A、B两点的抛物线解析式为y=x2+bx+c.
如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x-2与坐标轴分别交于A、B两点,过A、B两点的抛物线解析式为y=x2+bx+c.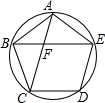 如图,A、B、C、D、E是⊙O上的五个等分点,连接AC、BE相交于点F.
如图,A、B、C、D、E是⊙O上的五个等分点,连接AC、BE相交于点F.