题目内容
4.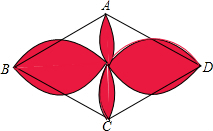 如图,四边形ABCD是菱形,AB=10cm,∠ABC=60°,分别以ABCD的四条边为直径作半圆.求图中红色部分的面积.
如图,四边形ABCD是菱形,AB=10cm,∠ABC=60°,分别以ABCD的四条边为直径作半圆.求图中红色部分的面积.
分析 连接AC、BD交于点O,记弓形BmO的面积为S1,弓形CnO的面积为S2,则S阴=4(S1+S2),再根据S1+S2=S半圆-S△BOC即可解决问题.
解答 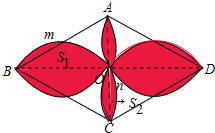 解:如图,连接AC、BD交于点O,记弓形BmO的面积为S1,弓形CnO的面积为S2,则S阴=4(S1+S2).
解:如图,连接AC、BD交于点O,记弓形BmO的面积为S1,弓形CnO的面积为S2,则S阴=4(S1+S2).
∵四边形ABCD是菱形,AB=10cm,∠ABC=60°,
∴AB=BC=10,△ABC是等边三角形,
∴BO=5$\sqrt{3}$,OC=5,
∵S1+S2=S半圆-S△BOC,
∴S阴=4(S1+S2)=4($\frac{1}{2}$•π•25-$\frac{25\sqrt{3}}{2}$)=(50π-50$\sqrt{3}$)cm2.
点评 本题考查菱形的性质、等边三角形的判定和性质、弓形面积、圆面积等知识,发现S阴=4(S1+S2)是解题的关键,属于中考面积问题中常考题型.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
12.下列说法正确的是( )
| A. | “明天会下雨”是必然事件 | |
| B. | 想了解“五•一”期间福州市各家庭的消费情况,适合的调查方式是抽样调查 | |
| C. | 正方形是轴对称图形,不是中心对称图形 | |
| D. | 120000用科学记数法表示是1.2×106 |
16.有四张正面分别标有数字-2,-6,2,6的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中抽取一张,将该卡片上的数字记为a;不放回,再从中抽取一张,将该卡片上的数字记为b,则使关于x的不等式组$\left\{\begin{array}{l}{\frac{3x-2}{2}<x+\frac{5}{2}}\\{ax>b}\end{array}\right.$的解集中有且只有3个非负整数解的概率( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
13.在下列6个图形中,每个小四边形都是全等的正方形,那么沿其正方形相邻边折叠,能够围成正方体的编号是( )
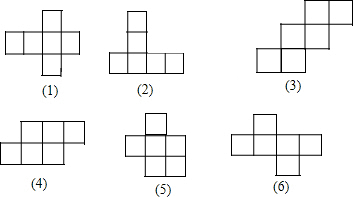

| A. | ①②③④ | B. | ①②⑥ | C. | ①③④ | D. | ①③⑥ |
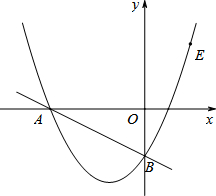 如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x-2与坐标轴分别交于A、B两点,过A、B两点的抛物线解析式为y=x2+bx+c.
如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x-2与坐标轴分别交于A、B两点,过A、B两点的抛物线解析式为y=x2+bx+c.