题目内容
19.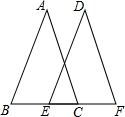 如图所示,AB=DE,AC=DF,BC=EF,小雪根据这些条件得出了四个结论,你认为叙述正确的个数是:(1)AB∥DE;(2)AC∥DF;(3)BE=CF;(4)∠DEF=∠ACB.( )
如图所示,AB=DE,AC=DF,BC=EF,小雪根据这些条件得出了四个结论,你认为叙述正确的个数是:(1)AB∥DE;(2)AC∥DF;(3)BE=CF;(4)∠DEF=∠ACB.( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据线段的和差得到BE=CF,根据已知条件得到△ABC≌△DEF,根据全等三角形的性质得到∠B=∠DEF,∠ACB=∠F,∠A=∠D,由平行线的判定定理得到AB∥DE,AC∥DF,根据三角形的内角和得到∠DEF=∠ACB,于是得到结论.
解答 解:∵BC=EF,
∴BC-CE=EF-CE,
即BE=CF,
在△ABC与△DEF中,$\left\{\begin{array}{l}{AB=DE}\\{AC=DF}\\{BC=EF}\end{array}\right.$,
∴△ABC≌△DEF,
∴∠B=∠DEF,∠ACB=∠F,∠A=∠D,
∴AB∥DE,AC∥DF,
∵∠DEF=180°-∠D-∠F,∠ACB=180°-∠A-∠B,
∴∠DEF=∠ACB,
∴正确的个数是4个,
故选D.
点评 本题考查的是全等三角形的性质和判定,平行线的判定,掌握全等三角形的对应边相等、全等三角形的对应角相等是解题的关键.

练习册系列答案
相关题目
9.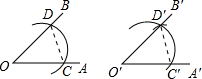 尺规作图作一个等于已知角的示意图如图,则要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( )
尺规作图作一个等于已知角的示意图如图,则要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( )
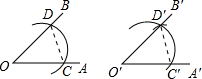 尺规作图作一个等于已知角的示意图如图,则要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( )
尺规作图作一个等于已知角的示意图如图,则要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( )| A. | SSS | B. | SAS | C. | ASA | D. | AAS |
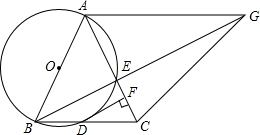 如图,在△ABC中,AB=AC,以AB为直径的圆O交BC于点D,交AC于点E,过点D作DF⊥AC,垂足为F.
如图,在△ABC中,AB=AC,以AB为直径的圆O交BC于点D,交AC于点E,过点D作DF⊥AC,垂足为F. 如图所示,AD是△ABC的中线,在AD及其延长线上截取DE=DF,连接CE、BF,试判断△BDF与△CDE全等吗?BF与CE有何位置关系?并说明原因.
如图所示,AD是△ABC的中线,在AD及其延长线上截取DE=DF,连接CE、BF,试判断△BDF与△CDE全等吗?BF与CE有何位置关系?并说明原因.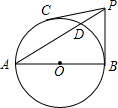 如图,AB是⊙O的直径,PB、PC是⊙O的切线,切点为B、C,连接PA交⊙O于D,∠BPC=2∠A.
如图,AB是⊙O的直径,PB、PC是⊙O的切线,切点为B、C,连接PA交⊙O于D,∠BPC=2∠A.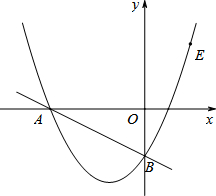 如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x-2与坐标轴分别交于A、B两点,过A、B两点的抛物线解析式为y=x2+bx+c.
如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x-2与坐标轴分别交于A、B两点,过A、B两点的抛物线解析式为y=x2+bx+c.