Question

20．如图，将?ABCD沿EF折叠，点A与点C重合，点D落在点C处，若AB=6，BC=4，∠B=60°，则△CEF的面积为$\frac{7\sqrt{3}}{2}$．

Answer 1

分析 过E点作EP⊥BC于P，设BP=m，则BE=2m，通过解直角三角形求得EP=$\sqrt{3}$ m，然后根据折叠的性质和勾股定理求得EC，进而根据三角形的面积就可求得；

解答 解：过E点作EP⊥BC于P，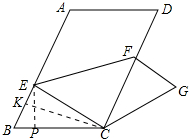
∵四边形ABCD是平行四边形，
∴AD=BC，∠D=∠B，∠A=∠BCD，
由折叠可知，AD=CG，∠D=∠G，∠A=∠ECG，
∴BC=GC，∠B=∠G，∠BCD=∠ECG，
∴∠BCE=∠GCF，
在△BCE和△GCF中，
$\left\{\begin{array}{l}{∠B=∠G}\\{∠BCE=∠GCF}\\{BC=GC}\end{array}\right.$，
∴△BCE≌△GCF（ASA）；
∵∠B=60°，∠EPB=90°，
∴∠BEP=30°，
∴BE=2BP，
设BP=m，则BE=2m，
∴EP=BE•sin60°=2m×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$ m，
由折叠可知，AE=CE，
∵AB=6，
∴AE=CE=6-2m，
∵BC=4，
∴PC=4-m，
在RT△ECP中，由勾股定理得（4-m）²+（$\sqrt{3}$ m）²=（6-2m）²，解得m=$\frac{5}{4}$，
∴EC=6-2m=6-2×$\frac{5}{4}$=$\frac{7}{2}$，
∵△BCE≌△GCF，
∴CF=EC=$\frac{7}{2}$，
∴S_△CEF=$\frac{1}{2}$×$\frac{7}{2}$×2$\sqrt{3}$=$\frac{7\sqrt{3}}{2}$．
故答案为$\frac{7\sqrt{3}}{2}$．

点评 本题是四边形综合题，考查了解直角三角形，平行四边形的性质，折叠的性质勾股定理的应用，三角形相似的判定和性质，三角形面积等，熟练掌握性质定理是解题的关键．