题目内容
16.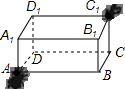 如图,有一长为6cm,宽为5cm,高为3cm的长方体,在它的底面A点有一只蚂蚁.
如图,有一长为6cm,宽为5cm,高为3cm的长方体,在它的底面A点有一只蚂蚁.(1)它想吃到上底面上与A点相对的C1点处的食物,需要爬行的最短路程是多少?画出图形,说明理由.
(2)当食物从C1点移到E点,B1E=2cm时,蚂蚁怎么走路最短?画出图形,说明理由.
(3)当蚂蚁在点,食物在E,AF=4cm,B1E=2cm,蚂蚁爬行最短路线为10m.
分析 将长方体展开,得到两种较短路径,找出两种路径中最短的即可.
解答  解:(1)如图2,∵AB=6cm,BC=5cm,AA1=3cm,
解:(1)如图2,∵AB=6cm,BC=5cm,AA1=3cm,
∴CC1=3cm,
∴AC1=$\sqrt{1{1}^{2}+{3}^{2}}$=$\sqrt{130}$(cm),
如图3,∵AB=6cm,BC=5cm,AA1=3cm,
∴AC1=$\sqrt{{6}^{2}{+8}^{2}}$=10(cm),
故由顶点A沿长方体表面到顶点C1,最短路线长为10cm.
故答案为10.
点评 本题考查平面展开-最短问题,解题的关键是把立体图形转化为平面图形解决,注意展开图有三种可能,其中两种是相同的,考虑问题要全面,属于中考常考题型.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
6.下列计算正确的是( )
| A. | a3+a5=a8 | B. | a4•a5=a20 | C. | (-2a3)2=4a6 | D. | a6÷a2=a3 |
7.下列计算正确的是( )
| A. | x2+x2=2x4 | B. | x2•x3=x6 | C. | (a+1)2=a2+1 | D. | (-x)8÷x2=x6 |
4.下列根式中属于最简二次根式的是( )
| A. | $\sqrt{{a}^{2}+1}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{12}$ | D. | $\sqrt{27}$ |
8.下列说法中,正确的是( )
| A. | $\sqrt{16}$等于±4 | B. | -42的平方根是±4 | C. | 8的立方根是±2 | D. | -$\sqrt{5}$是5的平方根 |
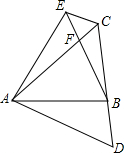 已知△ABC,将边AC绕点A顺时旋转60°得到AD,将AB绕点A逆时针旋转60°得到AE连接CD,CE,且点B在CD上
已知△ABC,将边AC绕点A顺时旋转60°得到AD,将AB绕点A逆时针旋转60°得到AE连接CD,CE,且点B在CD上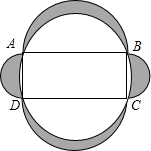 如图,已知矩形ABCD,且AB=12,AD=5.分别以AB、BC、CD、AD为直径画半圆;再以矩形ABCD的对角线AC为直径画圆,此圆通过A、B、C,D四点,则斜线部分面积为( )
如图,已知矩形ABCD,且AB=12,AD=5.分别以AB、BC、CD、AD为直径画半圆;再以矩形ABCD的对角线AC为直径画圆,此圆通过A、B、C,D四点,则斜线部分面积为( )