题目内容
 如图,已知∠AOC=∠DOE=90°,OF平分∠AOD,OB平分∠COE.
如图,已知∠AOC=∠DOE=90°,OF平分∠AOD,OB平分∠COE.(1)∠BOF的度数是多少?说明理由;
(2)如果∠AOF=15°,那么∠DOB等于多少度?说明理由.
考点:角的计算,角平分线的定义
专题:
分析:(1)根据余角的性质可得∠AOD=∠COE,根据角平分线的性质和等量关系可得∠FOD=∠COB,依此即可求得∠BOF的度数;(2)
解答:解:(1)∵∠AOC=∠DOE=90°,
∴∠AOD+∠COD=∠COE+∠COD
∴∠AOD=∠COE,
∵OF平分∠AOD,OB平分∠COE,
∴∠FOA=
∠AOD,∠COB=
∠COE,
∴∠FOA=∠COB,
∴∠AOF+∠COF=∠COB+∠COF,
即∠BOF=∠AOC=90°;
(2)∵∠AOF=15°,
∴∠DOF=15°,
由(1)得∠BOF=90°,
∴∠DOB=∠BOF-∠DOF=90°-15°=75°.
∴∠AOD+∠COD=∠COE+∠COD
∴∠AOD=∠COE,
∵OF平分∠AOD,OB平分∠COE,
∴∠FOA=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠FOA=∠COB,
∴∠AOF+∠COF=∠COB+∠COF,
即∠BOF=∠AOC=90°;
(2)∵∠AOF=15°,
∴∠DOF=15°,
由(1)得∠BOF=90°,
∴∠DOB=∠BOF-∠DOF=90°-15°=75°.
点评:本题主要考查了角平分线定义,余角的性质和角的有关计算的应用,关键是求出∠FOD=∠COB.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 如图所示,把一张长方形的纸片沿着AB折叠,若∠1=50°.则∠2的度数为( )
如图所示,把一张长方形的纸片沿着AB折叠,若∠1=50°.则∠2的度数为( )| A、40° | B、50° |
| C、65° | D、75° |
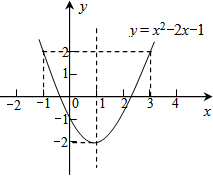 已知二次函数y=x2-2x-1的图象如图所示,根据图中提供的信息,求使得y≤2成立的x的取值范围是( )
已知二次函数y=x2-2x-1的图象如图所示,根据图中提供的信息,求使得y≤2成立的x的取值范围是( )| A、x≤-1或x≥3 |
| B、-2≤x≤2 |
| C、x≥-2 |
| D、-1≤x≤3 |
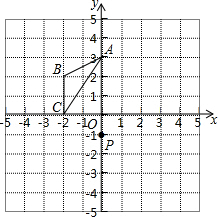 如图,△ABC的位置如图,
如图,△ABC的位置如图, 如图,等腰△ABC中,AB=AC,BC∥x轴,点A.C在反比例函数y=
如图,等腰△ABC中,AB=AC,BC∥x轴,点A.C在反比例函数y=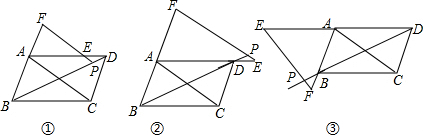
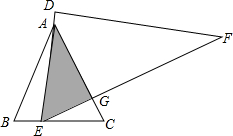 如图,等边△ABC中,AB=6,将一直角三角板DEF的60°角的顶点E置于边BC上移动(不与B、C重合),移动过程中,始终满足直角边DE经过点A,斜边EF交AC于点G.
如图,等边△ABC中,AB=6,将一直角三角板DEF的60°角的顶点E置于边BC上移动(不与B、C重合),移动过程中,始终满足直角边DE经过点A,斜边EF交AC于点G. 如图是一个多边形,求∠A1+∠A2+∠A3+…+∠A23+∠A24的度数.
如图是一个多边形,求∠A1+∠A2+∠A3+…+∠A23+∠A24的度数.