题目内容
9.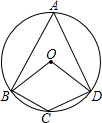 如图,四边形ABCD是⊙O的内接四边形,若∠C=140°,则∠BOD=80度.
如图,四边形ABCD是⊙O的内接四边形,若∠C=140°,则∠BOD=80度.
分析 先根据圆内接四边形的性质得到∠A=180°-∠C=50°,然后根据圆周角定理求∠BOD.
解答 解:∵∠A+∠C=180°,
∴∠A=180°-140°=40°,
∴∠BOD=2∠A=80°.
故答案为80.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了圆内接四边形的性质.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
19.如图(1)是两圆柱形联通容器(联通外体积忽略不计).向甲容器匀速注水,甲容器的水面高度h(cm)随时间t(分)之间的函数关系如图(2)所示,根据提供的图象信息,若甲的底面半径为1cm,则乙容器底面半径为( )
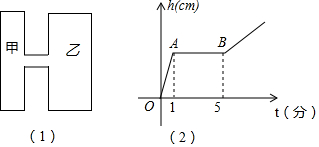

| A. | 5cm | B. | 4cm | C. | 3cm | D. | 2cm |
4.若等腰三角形中有两边长分别为3和7,则这个三角形的周长为( )
| A. | 13 | B. | 17 | C. | 10或13 | D. | 13或17 |
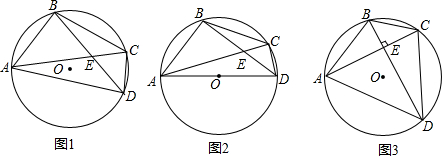
 如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F.
如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F.