题目内容
18. 如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F.
如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F.(1)求证:△ABE≌△FCE;
(2)过点D作DG⊥AE于点G,H为DG的中点.判断CH与DG的位置关系,并说明理由.
分析 (1)根据平行四边形的性质,利用ASA即可证明.
(2)结论:CH⊥DG.利用三角形中位线定理,证明CH∥AF即可解决问题.
解答 解:(1)∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,
∴∠B=∠ECF
∵E为BC的中点,
∴BE=CE,
在△ABE和△FCE中,
$\left\{\begin{array}{l}{∠B=∠ECF}\\{BE=EC}\\{∠AEB=∠FEC}\end{array}\right.$
∴△ABE≌△FCE.
(2)结论:CH⊥DG.理由如下:
∵△ABE≌△FCE,
∴AB=CF,
∵AB=CD,
∴DC=CF,
∵H为DG的中点,
∴CH∥FG
∵DG⊥AE,
∴CH⊥DG.
点评 本题考查平行四边形的性质、全等三角形的判定和性质,三角形的中位线定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.函数y=$\sqrt{x+1}$中自变量x的取值范围是( )
| A. | x>-1 | B. | x≥-1 | C. | x<-1 | D. | x≤-1 |
3.不等式组$\left\{\begin{array}{l}{-x+1≤0}\\{\frac{1}{4}x-1<0}\end{array}\right.$的所有整数解的和是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
10. 甲、乙两车从A城出发前往B城,在整个行程中,两车离开A城的距离y与t的对应关系如图所示,下列说法正确的说法有( )
甲、乙两车从A城出发前往B城,在整个行程中,两车离开A城的距离y与t的对应关系如图所示,下列说法正确的说法有( )
(1)A、B两城之间距离是300千米(2)甲车的速度是60千米/小时
(3)乙车出发4小时追上甲车(4)甲车出发2小时或3小时,两车相距20千米.
 甲、乙两车从A城出发前往B城,在整个行程中,两车离开A城的距离y与t的对应关系如图所示,下列说法正确的说法有( )
甲、乙两车从A城出发前往B城,在整个行程中,两车离开A城的距离y与t的对应关系如图所示,下列说法正确的说法有( )(1)A、B两城之间距离是300千米(2)甲车的速度是60千米/小时
(3)乙车出发4小时追上甲车(4)甲车出发2小时或3小时,两车相距20千米.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.$\frac{1}{4}$的相反数等于( )
| A. | $-\frac{1}{4}$ | B. | 4 | C. | $\frac{1}{4}$ | D. | ±$\frac{1}{4}$ |
8.下列各数中,比-2小1的数是( )
| A. | -1 | B. | -3 | C. | 3 | D. | 1 |
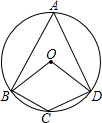 如图,四边形ABCD是⊙O的内接四边形,若∠C=140°,则∠BOD=80度.
如图,四边形ABCD是⊙O的内接四边形,若∠C=140°,则∠BOD=80度.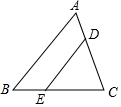 如图所示,△ABC中,点D、E分别是AC、BC边上的点,且DE∥AB,CD:CA﹦2:3,△ABC的面积是18,则四边形ABED的面积是( )
如图所示,△ABC中,点D、E分别是AC、BC边上的点,且DE∥AB,CD:CA﹦2:3,△ABC的面积是18,则四边形ABED的面积是( )